Из истории квадратных уравнений а квадратные уравнения в древнем вавилоне. Из истории возникновения квадратных уравнений
Из истории квадратных уравнений .а) Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Применяя современную алгебраическую запись, можно сказать , что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
х 2 + х = , х 2 – х = 14
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным , однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
В «Арифметике» Диофанта нет систематического изложения алгебры , однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение - 96».
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны , то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х. Другое же меньше, т. е. 10 - х. Разность между ними 2х. Отсюда уравнение:
(10+x)(10-x) =96,
или же
100 -x 2 = 96.
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = - 2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел , то можно прийти к решению уравнения:
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.
б) Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабахаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме
ах 2 + b х = с, а > 0
В уравнении коэффициенты , кроме а , могут быть отрицательными. Правило Брахмагупта по существу совпадает с нашим.
В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 3.
Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.
Соответствующее задаче 3 уравнение:
Бхаскара пишет под видом:
x 2 - 64x = - 768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:
x 2 - б4х + 32 2 = -768 + 1024,
(х - 32) 2 = 256,
x 1 = 16, x 2 = 48.
в) Квадратные уравнения у Аль-Хорезми
В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
«Квадраты равны корням», т. е. ах 2 = bх.
«Квадраты равны числу», т. е. ах 2 = с.
«Корни равны числу», т. е. ах = с.
«Квадраты и числа равны корням», т. е. ах 2 + с = bх.
«Квадраты и корни равны числу», т. е. ах 2 + bх =с.
«Корни и числа равны квадратам», т. е. bх + с == ах 2 .
Приведем пример.
Задача 4. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х 2 + 21 = 10х).
Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя , от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
г) Квадратные уравнения в Европе XIII-XVII вв.
Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. Итальянским математиком Леонардо Фибоначчи. Этот объемный труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой , и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники XVI-XVII вв. и частично XVIII.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду
х 2 + bх = с,
при всевозможных комбинациях знаков коэффициентов b , с было сформулировано в Европе лишь в 1544 г. М.Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета , однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера , решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX-VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения , составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.
Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI-Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака. А затем европейскими математиками Возрождения , в итоге длительного поиска создавшими язык современной алгебры, использование букв, введение символов арифметических операций, скобок и т. д. На рубеже XVI-XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения , была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.
Итак, ввиду важности и обширности материала, связанного с понятием уравнения , его изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.
Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
X 2 + X = ѕ; X 2 - X = 14,5
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Как составлял и решал Диофант квадратные уравнения.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение - 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х , другое же меньше, т.е. 10 - х . Разность между ними 2х .
Отсюда уравнение:
(10 + х)(10 - х) = 96
Отсюда х = 2 . Одно из искомых чисел равно 12 , другое 8 . Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
у(20 - у) = 96,
у 2 - 20у + 96 = 0. (2)
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ах 2 + bх = с, а > 0. (1)
В уравнении (1) коэфиценты, кроме а , могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 13.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 3).
Соответствующее задаче 13 уравнение:
(x/8) 2 + 12 = x
Бхаскара пишет под видом:
х 2 - 64х = -768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:
х 2 - 64х + 32 2 = -768 + 1024,
(х - 32) 2 = 256,
х - 32 = ± 16,
х 1 = 16, х 2 = 48.
1.1. Из истории возникновения квадратных уравнений
Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.
Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение - 96».
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х. Другое же меньше, т. е. 10 - х. Разность между ними 2х. Отсюда уравнение:
(10+x)(10-x) =96,
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = - 2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то можно прийти к решению уравнения:
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ax 2 + bх = с, а> 0. (1)
В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.
Соответствующее задаче 3 уравнение:
Бхаскара пишет под видом:
x 2 - 64x = - 768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:
x 2 - б4х + 32 2 = -768 + 1024,
(х - 32) 2 = 256,
x 1 = 16, x 2 = 48.
Квадратные уравнения у Аль-Хорезми
В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корням», т. е. ах 2 = bх.
2) «Квадраты равны числу», т. е. ах 2 = с.
3) «Корни равны числу», т. е. ах = с.
4) «Квадраты и числа равны корням», т. е. ах 2 + с = bх.
5) «Квадраты и корни равны числу», т. е. ах 2 + bх =с.
6) «Корни и числа равны квадратам», т. е. bх + с == ах 2 .
Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Приведем пример.
Задача 4. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х 2 + 21 = 10х).
Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
Квадратные уравнения в Европе XII-XVII в.
Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.
Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x 2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М.Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид..
Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX-VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.
Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI-Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака. А затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры, использование букв, введение символов арифметических операций, скобок и т. д. На рубеже XVI-XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.
Итак, ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования.
Ковальчук Кирилл
Проект "Квадратные уравнения через века и страны" знакомит учащихся с учеными математики, открытия которых являются основой научно-технического прогресса, развивает интерес к математике как к предмету на основе знакомства с историческим материалом, расширяет кругозор учащихся, стимулирует их познавательную активность и творчество.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Проектная работа ученика 8 класса МОУ СОШ №17 с.Борисовка Ковальчука Кирилла Руководитель Мулюкова Г.В.
Квадратные уравнения через века и страны
Цель проекта: Познакомить учащихся с учеными математики, открытия которых являются основой научно-технического прогресса. Показать значимость работ ученых для развития геометрии и физики.??????????? Наглядно продемонстрировать применение научных открытий в жизни. Развивать интерес к математике как к предмету на основе знакомства с историческим материалом. Расширять кругозор учащихся, стимулировать их познавательную активность и творчество
Необходимость решать уравнения не только первой степени, но и второй ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Правила решения этих уравнений, изложенные в вавилонских текстах, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
. (ок. 365 - 300 г. до н.э.) - древнегреческий математик, автор первых дошедших до нас теоретических трактатов по математике. Евклид, или Эвклид
Евклид Начала Там, где с морем Сливается Нил, В древнем жарком краю Пирамид Математик греческий жил - Многознающий, Мудрый Эвклид. Геометрию он изучал, Геометрии он обучал. Написал он великий труд. Эту книгу «Начала» зовут.
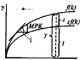
Евклид 3 век до н.э. Евклид решал квадратные уравнения, применяя геометрический способ. Вот одна из задач из древнегреческого трактата: «Имеется город с границей в виде квадрата со стороной неизвестного размера, в центре каждой стороны находятся ворота. На расстоянии 20бу(1бу=1,6м) от северных ворот стоит столб. Если пройти от южных ворот 14бу прямо, затем повернуть на запад и пройти еще 1775бу, то можно увидеть столб. Спрашивается: какова сторона границы города? »
Чтобы определить неизвестную сторону квадрата, получаем квадратное уравнение x ² +(k+l)x-2kd =0 . В данном случае уравнение имеет вид x ² +34x-71000=0 , откуда х=250бу l x d k
Квадратные уравнения в Индии Задачи на квадратные уравнения встречаются и в астрономическом трактате « Ариабхаттиам », составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта, изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ax ² +bx=c , a>0 В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».
Одна из задач знаменитого индийского математика XІІ века Бхаскары Обезьянок резвых стая Всласть поевши, развлекалась. Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам… Стали прыгать повисая… Сколько было обезьянок Ты скажи мне, в этой стае?.
Решение. () 2 +12 = х, х 2 - 64х +768 = 0, а =1, в = -64, с = 768, тогда Д = (-64) 2 -4·1·768 = 1024 > 0. Х 1 , 2 = , х 1 = 48, х 2 = 16. Ответ.Обезьян было 16 или 48. Давайте решим её.
Формула корней квадратного уравнения « переоткрывалась » неоднократно. Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте. Среднеазиатский ученый ал-Хорезми в трактате « Китаб аль-джерб валь-мукабала » получил эту формулу методом выделения полного квадрата.
Как же решал ал-Хорезми это уравнение. Он писал: "Правило таково: раздвои число корней, х=2х · 5 получите в этой задаче пять, 5 умножь на это равное ему, будет двадцать пять, 5 · 5=25 прибавь это к тридцати девяти, 25+39 будет шестьдесят четыре, 64 извлеки из этого корень, будет восемь, 8 и вычти из этого половину числа корней, т.е.пять, 8- 5 останется три- это и 3 Будет корень квадрата, который ты искал." А второй корень? Второй корень не находили, так как отрицательные числа не были известны. х 2 +10 х = 39
Квадратные уравнения в Европе 13-17вв. Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники 16-17вв. и частично 18.
Франсуа Виет – крупнейший математик 16 века
До Ф. Виета решение квадратного уравнения выполнялось по своим правилам в виде очень длинных словесных рассуждений и описаний, довольно громоздких действий. Даже само уравнение не могли записать, для этого требовалось довольно длинное и сложное словесное описание. Он ввел термин «коэффициент». Предложил искомые величины обозначать гласными, а данные – согласными. Благодаря символике Виета можно записать квадратное уравнение в виде: ax 2 + bx + c =0 . Теорема: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Несмотря на то, что эта теорема называется «Теорема Виета», она была известна и до него, а он только преобразовал ее в современный вид. Виета называют «отцом алгебры»
Человечество прошло длительный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание все более полным и совершенным. Заключительное слово
Нас, живущих в начале XXI века, влечет старина. В своих предках мы замечаем прежде всего то, чего им не хватает с современной точки зрения, и обычно не замечаем того, что нам самим не хватает по сравнению с ними.
Не будем и мы забывать о них…
СПАСИБО ЗА внимание!
Как составлял и решал Диофант квадратные уравнения. Отсюда уравнение: (10+х)(10 -х) =96 или же: 100 - х2 =96 х2 - 4=0 (1) Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Src="https://present5.com/presentation/137369579_55459696/image-4.jpg" alt="Квадратные уравнения в Индии. ах2 + bх = с, а>0. (1) "> Квадратные уравнения в Индии. ах2 + bх = с, а>0. (1)
Квадратные уравнения у ал – Хорезми. 1) «Квадраты равны корнями» , т. е. ах2 + с = bх. 2) «Квадраты равны числу» , т. е. ах2 = с. 3) «Корни равны числу» , т. е. ах = с. 4) «Квадраты и числа равны корням» , т. е. ах2 + с = bх. 5) «Квадраты и корни равны числу» , т. е. ах2 + bx = с. 6) «Корни и числа равны квадратам» , т. е. bx + с = ах2.
Квадратные уравнения в Европе ХIII ХVII вв. х2 +bх = с, при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
О теореме Виета. «Если В + D, умноженное на А - А 2, равно ВD, то А равно В и равно D» . На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место (а + b)х - х2 = ab, т. е. х2 - (а + b)х + аb = 0, то х1 = а, х2 = b.
Способы решения квадратных уравнений. 1. СПОСОБ: Разложение левой части уравнения на множители. Решим уравнение х2 + 10 х - 24 = 0. Разложим левую часть на множители: х2 + 10 х - 24 = х2 + 12 х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2). Следовательно, уравнение можно переписать так: (х + 12)(х - 2) = 0 Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = - 12. Это означает, что число 2 и - 12 являются корнями уравнения х2 + 10 х - 24 = 0.
2. СПОСОБ: Метод выделения полного квадрата. Решим уравнение х2 + 6 х - 7 = 0. Выделим в левой части полный квадрат. Для этого запишем выражение х2 + 6 х в следующем виде: х2 + 6 х = х2 + 2 х 3. полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как х2 + 2 х 3 + 32 = (х + 3)2. Преобразуем теперь левую часть уравнения х2 + 6 х - 7 = 0, прибавляя к ней и вычитая 32. Имеем: х2 + 6 х - 7 = х2 + 2 х 3 + 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16. Таким образом, данное уравнение можно записать так: (х + 3)2 - 16 =0, (х + 3)2 = 16. Следовательно, х + 3 - 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
3. СПОСОБ: Решение квадратных уравнений по формуле. Умножим обе части уравнения ах2 + bх + с = 0, а ≠ 0 на 4 а и последовательно имеем: 4 а 2 х2 + 4 аbх + 4 ас = 0, ((2 ах)2 + 2 ах b + b 2) - b 2 + 4 ac = 0, (2 ax + b)2 = b 2 - 4 ac, 2 ax + b = ± √ b 2 - 4 ac, 2 ax = - b ± √ b 2 - 4 ac,
4. СПОСОБ: Решение уравнений с использованием теоремы Виета. Как известно, приведенное квадратное уравнение имеет вид х2 + px + c = 0. (1) Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид x 1 x 2 = q, x 1 + x 2 = - p а) x 2 – 3 x + 2 = 0; x 1 = 2 и x 2 = 1, так как q = 2 > 0 и p = - 3 0 и p= 8 > 0. б) x 2 + 4 x – 5 = 0; x 1 = - 5 и x 2 = 1, так как q= - 5 0; x 2 – 8 x – 9 = 0; x 1 = 9 и x 2 = - 1, так как q = - 9
5. СПОСОБ: Решение уравнений способом «переброски» . Рассмотрим квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. Умножая обе его части на а, получаем уравнение а 2 х2 + аbх + ас = 0. Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у2 + by + ас = 0, равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = у1/а и х1 = у2/а.
Пример. Решим уравнение 2 х2 – 11 х + 15 = 0. Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у2 – 11 у + 30 = 0. Согласно теореме Виета у1 = 5 у2 = 6 х1 = 5/2 x 2 = 6/2 Ответ: 2, 5; 3. x 1 = 2, 5 x 2 = 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения. А. Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. 1) Если, а+ b + с = 0 (т. е. сумма коэффициентов равна нулю), то х1 = 1, х2 = с/а. Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение x 2 + b/a x + c/a = 0. Согласно теореме Виета x 1 + x 2 = - b/a, x 1 x 2 = 1 c/a. По условию а – b + с = 0, откуда b = а + с. Таким образом, x 1 + x 2 = - а + b/a= -1 – c/a, x 1 x 2 = - 1 (- c/a), т. е. х1 = -1 и х2 = c/a, что и требовалось доказать.
Б. Если второй коэффициент b = 2 k – четное число, то формулу корней В. Приведенное уравнение х2 + рх + q= 0 совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней
7. СПОСОБ: Графическое решение квадратного уравнения. Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = - px - q. Построим графики зависимости у = х2 и у = - px - q.
Пример 1) Решим графически уравнение х2 - 3 х - 4 = 0 (рис. 2). Решение. Запишем уравнение в виде х2 = 3 х + 4. Построим параболу у = х2 и прямую у = 3 х + 4. Прямую у = 3 х + 4 можно построить по двум точкам М (0; 4) и N (3; 13). Ответ: х1 = - 1; х2 = 4
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки. нахождения корней квадратного циркуля и линейки (рис. 5). уравнения Тогда по теореме о секущих имеем OB OD = OA OC, откуда OC = OB OD/ OA= х1 х2/ 1 = c/a. ах2 + bх + с = 0 с помощью
Src="https://present5.com/presentation/137369579_55459696/image-19.jpg" alt="1) Радиус окружности больше ординаты центра (AS > SK, или R > a +"> 1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2 a), окружность пересекает ось Ох в двух точках (6, а рис.) В(х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения ах2 + bх + с = 0. 2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2 a), окружность касается оси Ох (рис. 6, б) в точке В(х1; 0), где х1 - корень квадратного уравнения. 3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис. 6, в), в этом случае уравнение не имеет решения.
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы. z 2 + pz + q = 0. Криволинейная шкала номограммы построена по формулам (рис. 11): Полагая ОС = р, ED = q, ОЕ = а (все в см.), Из подобия треугольников САН и CDF получим пропорцию
Примеры. 1) Для уравнения z 2 - 9 z + 8 = 0 номограмма дает корни z 1 = 8, 0 и z 2 = 1, 0 (рис. 12). 2) Решим с помощью номограммы уравнение 2 z 2 - 9 z + 2 = 0. Разделим коэффициенты этого уравнения на 2, получим уравнение z 2 - 4, 5 z + 1 = 0. Номограмма дает корни z 1 = 4 и z 2 = 0, 5. 3) Для уравнения z 2 - 25 z + 66 = 0 коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5 t, получим уравнение t 2 - 5 t + 2, 64 = 0, которое решаем посредством номограммы и получим t 1 = 0, 6 и t 2 = 4, 4, откуда z 1 = 5 t 1 = 3, 0 и z 2 = 5 t 2 = 22, 0.
10. СПОСОБ: Геометрический способ решения квадратных уравнений. Примеры. 1) Решим уравнение х2 + 10 х = 39. В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39» (рис. 15). Для искомой стороны х первоначального квадрата получим
у2 + 6 у - 16 = 0. Решение представлено на рис. 16, где у2 + 6 у = 16, или у2 + 6 у + 9 = 16 + 9. Решение. Выражения у2 + 6 у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6 у - 16 + 9 - 9 = 0 - одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = - 8 (рис. 16).
Загрузка...
