Sequenze numeriche e metodi per assegnarle. Rappresentazione geometrica delle sequenze numeriche. Sequenza numerica e metodi per specificarla

Viene data la definizione di sequenza numerica. Vengono considerati esempi di successioni infinitamente crescenti, convergenti e divergenti. Si considera una successione contenente tutti i numeri razionali.

Definizione.
Sequenza numerica (xn) è una legge (regola) secondo la quale, per ogni numero naturale n = 1, 2, 3, . . . viene assegnato un certo numero x n.
L'elemento x n è chiamato l'ennesimo membro o elemento della sequenza.

La sequenza è indicata come l'ennesimo termine racchiuso tra parentesi graffe: . Sono possibili anche le seguenti denominazioni: . Indicano esplicitamente che l'indice n appartiene all'insieme dei numeri naturali e che la sequenza stessa ha un numero infinito di termini. Ecco alcune sequenze di esempio:
, , .

In altre parole, una sequenza numerica è una funzione il cui dominio di definizione è l'insieme dei numeri naturali. Il numero di elementi della sequenza è infinito. Tra gli elementi possono esserci anche membri che hanno gli stessi significati. Inoltre, una sequenza può essere considerata come un insieme numerato di numeri costituito da un numero infinito di membri.

A noi interesserà principalmente la questione di come si comportano le successioni quando n tende all'infinito: . Questo materiale è presentato nella sezione Limite di una sequenza: teoremi e proprietà di base. Qui vedremo alcuni esempi di sequenze.

Esempi di sequenza

Esempi di successioni infinitamente crescenti

Considera la sequenza. Il membro comune di questa sequenza è . Scriviamo i primi termini:
.
Si può vedere che all'aumentare del numero n gli elementi aumentano indefinitamente verso valori positivi. Possiamo dire che questa sequenza tende a: for .

Consideriamo ora una sequenza con un termine comune. Ecco i suoi primi membri:
.
Al crescere del numero n, gli elementi di questa sequenza aumentano illimitatamente in valore assoluto, ma non hanno segno costante. Cioè, questa sequenza tende a: a .

Esempi di successioni convergenti ad un numero finito

Considera la sequenza. Il suo membro comune. I primi termini hanno la seguente forma:
.
Si può vedere che all'aumentare del numero n gli elementi di questa sequenza si avvicinano al loro valore limite a = 0 : A . Quindi ogni termine successivo è più vicino allo zero del precedente. In un certo senso possiamo considerare che esiste un valore approssimativo per il numero a = 0 con errore. È chiaro che all'aumentare di n questo errore tende a zero, cioè scegliendo n l'errore può essere reso piccolo quanto si desidera. Inoltre, per ogni dato errore ε > 0 è possibile specificare un numero N tale che per tutti gli elementi con numeri maggiori di N:, la deviazione del numero dal valore limite a non superi l'errore ε:.

Quindi, considera la sequenza. Il suo membro comune. Ecco alcuni dei suoi primi membri:
.
In questa sequenza, i termini con numeri pari sono uguali a zero. I termini con n dispari sono uguali. Pertanto, all’aumentare di n, i loro valori si avvicinano al valore limite a = 0 . Ciò deriva anche dal fatto che
.
Proprio come nell'esempio precedente, possiamo specificare un errore ε arbitrariamente piccolo > 0 , per il quale è possibile trovare un numero N tale che gli elementi con numeri maggiori di N si discostino dal valore limite a = 0 per un importo non superiore all'errore specificato. Pertanto questa successione converge al valore a = 0 : A .

Esempi di sequenze divergenti

Consideriamo una sequenza con il seguente termine comune:

Ecco i suoi primi membri:


.
Si può vedere che i termini con numeri pari:
,
convergono al valore a 1 = 0 . Membri dispari:
,
convergono al valore a 2 = 2 . La sequenza stessa, al crescere di n, non converge ad alcun valore.

Sequenza con termini distribuiti nell'intervallo (0;1)

Ora diamo un'occhiata a una sequenza più interessante. Prendiamo un segmento sulla linea numerica. Dividiamolo a metà. Otteniamo due segmenti. Permettere
.
Dividiamo nuovamente ciascuno dei segmenti a metà. Otteniamo quattro segmenti. Permettere
.
Dividiamo nuovamente ogni segmento a metà. Prendiamo


.
E così via.

Di conseguenza, otteniamo una sequenza i cui elementi sono distribuiti in un intervallo aperto (0; 1) . Qualunque punto prendiamo dall'intervallo chiuso , possiamo sempre trovare membri della sequenza che saranno arbitrariamente vicini a questo punto o coincideranno con esso.

Quindi dalla sequenza originale si può selezionare una sottosequenza che convergerà in un punto arbitrario dell'intervallo . Cioè, all'aumentare del numero n, i membri della sottosequenza si avvicineranno sempre di più al punto prescelto.

Ad esempio, per il punto a = 0 è possibile scegliere la seguente sottosequenza:
.
= 0 .

Per il punto a = 1 Scegliamo la seguente sottosequenza:
.
I termini di questa sottosuccessione convergono al valore a = 1 .

Poiché esistono sottosuccessioni che convergono a valori diversi, la sequenza originale stessa non converge a nessun numero.

Successione contenente tutti i numeri razionali

Costruiamo ora una successione che contenga tutti i numeri razionali. Inoltre, ciascun numero razionale apparirà in tale sequenza un numero infinito di volte.

Il numero razionale r può essere rappresentato come segue:
,
dove è un numero intero; - naturale.
Dobbiamo associare ogni numero naturale n con una coppia di numeri p e q in modo che qualsiasi coppia p e q sia inclusa nella nostra sequenza.

Per fare ciò, disegna gli assi p e q sul piano. Disegniamo le linee della griglia attraverso i valori interi di p e q. Allora ogni nodo di questa griglia c corrisponderà ad un numero razionale. L'intero insieme dei numeri razionali sarà rappresentato da un insieme di nodi. Dobbiamo trovare un modo per numerare tutti i nodi in modo da non perderne nessuno. Questo è facile da fare se si numerano i nodi in quadrati, i cui centri si trovano nel punto (0; 0) (Guarda l'immagine). In questo caso le parti inferiori dei quadrati con q < 1 non ne abbiamo bisogno. Pertanto non sono mostrati nella figura.

Quindi, per il lato superiore del primo quadrato abbiamo:
.
Successivamente, numeriamo la parte superiore del quadrato successivo:

.
Numeriamo la parte superiore del seguente quadrato:

.
E così via.

In questo modo otteniamo una sequenza contenente tutti i numeri razionali. Puoi notare che qualsiasi numero razionale appare in questa sequenza un numero infinito di volte. Infatti, insieme al nodo , questa sequenza comprenderà anche i nodi , dove è un numero naturale. Ma tutti questi nodi corrispondono allo stesso numero razionale.

Quindi dalla sequenza che abbiamo costruito, possiamo selezionare una sottosuccessione (avente un numero infinito di elementi), i cui elementi sono tutti uguali ad un numero razionale predeterminato. Poiché la sequenza che abbiamo costruito ha sottosuccessioni che convergono a numeri diversi, la sequenza non converge a nessun numero.

Conclusione

Qui abbiamo dato una definizione precisa della sequenza numerica. Abbiamo anche sollevato la questione della sua convergenza, basata su idee intuitive. La definizione esatta di convergenza è discussa nella pagina Definizione del limite di una sequenza. Proprietà e teoremi correlati sono indicati nella pagina

Vita sì= F(X), X DI N, Dove N– un insieme di numeri naturali (o una funzione di un argomento naturale), denotato sì=F(N) O sì 1 ,sì 2 ,…, sì, no,…. Valori sì 1 ,sì 2 ,sì 3 ,… sono chiamati rispettivamente primo, secondo, terzo, ... membri della sequenza.

Ad esempio, per la funzione sì= N 2 si può scrivere:

sì 1 = 1 2 = 1;

sì 2 = 2 2 = 4;

sì 3 = 3 2 = 9;…y n = n 2 ;…

Metodi per specificare le sequenze. Le sequenze possono essere specificate in vari modi, tra i quali tre sono particolarmente importanti: analitico, descrittivo e ricorrente.

1. Una successione è data analiticamente se viene data la sua formula N° membro:

sì, no=F(N).

Esempio. sì, no= 2N - 1 – sequenza di numeri dispari: 1, 3, 5, 7, 9, …

2. Descrittivo Il modo per specificare una sequenza numerica è spiegare da quali elementi è costruita la sequenza.

Esempio 1. "Tutti i termini della sequenza sono uguali a 1." Ciò significa che stiamo parlando di una sequenza stazionaria 1, 1, 1, …, 1, ….

Esempio 2: "La sequenza è composta da tutti i numeri primi in ordine crescente." Pertanto, la sequenza data è 2, 3, 5, 7, 11, …. Con questo metodo di specificazione della sequenza in questo esempio, è difficile rispondere a cosa, ad esempio, è uguale il millesimo elemento della sequenza.

3. Il metodo ricorrente per specificare una sequenza consiste nel specificare una regola che consenta di eseguire il calcolo N-esimo membro di una sequenza se i suoi membri precedenti sono noti. Il nome metodo ricorrente deriva dalla parola latina ricorrente- ritorno. Molto spesso, in questi casi, viene indicata una formula che consente di esprimere N dall'esimo membro della sequenza fino ai precedenti e specificare 1–2 membri iniziali della sequenza.

Esempio 1. sì 1 = 3; sì n = sì n–1 + 4 se N = 2, 3, 4,….

Qui sì 1 = 3; sì 2 = 3 + 4 = 7;sì 3 = 7 + 4 = 11; ….

Come puoi vedere, la sequenza ottenuta in questo esempio può essere specificata anche analiticamente: sì, no= 4N - 1.

Esempio 2. sì 1 = 1; sì 2 = 1; sì, no = sì, no –2 + sì, no–1 se N = 3, 4,….

Qui: sì 1 = 1; sì 2 = 1; sì 3 = 1 + 1 = 2; sì 4 = 1 + 2 = 3; sì 5 = 2 + 3 = 5; sì 6 = 3 + 5 = 8;

La sequenza in questo esempio è studiata soprattutto in matematica perché ha una serie di proprietà e applicazioni interessanti. Si chiama sequenza di Fibonacci, dal nome del matematico italiano del XIII secolo. È molto facile definire la sequenza di Fibonacci in modo ricorrente, ma molto difficile analiticamente. N L'esimo numero di Fibonacci si esprime attraverso il suo numero seriale mediante la seguente formula.

A prima vista, la formula per N l'esimo numero di Fibonacci sembra poco plausibile, poiché la formula che specifica la sequenza dei numeri naturali contiene solo radici quadrate, ma è possibile verificare “manualmente” la validità di questa formula per i primi N.

Proprietà delle sequenze numeriche.

Una sequenza numerica è un caso speciale di una funzione numerica, pertanto per le sequenze vengono considerate anche alcune proprietà delle funzioni.

Definizione . Sotto sequenza ( sì, no} si dice crescente se ciascuno dei suoi termini (eccetto il primo) è maggiore del precedente:

sì 1 sì 2 sì 3 sì no sì n +1

Definizione.Sequenza ( sì, no} si dice decrescente se ciascuno dei suoi termini (eccetto il primo) è minore del precedente:

sì 1 > sì 2 > sì 3 > … > sì, no> sì, no +1 > … .

Le sequenze crescenti e decrescenti sono combinate sotto il termine comune: sequenze monotone.

Esempio 1. sì 1 = 1; sì, no= N 2 – sequenza crescente.

Pertanto è vero il seguente teorema (una proprietà caratteristica di una progressione aritmetica). Una sequenza numerica è aritmetica se e solo se ciascuno dei suoi membri, tranne il primo (e l'ultimo nel caso di una sequenza finita), è uguale alla media aritmetica dei membri precedenti e successivi.

Esempio. A quale valore X numeri 3 X + 2, 5X– 4 e 11 X+ 12 formano una progressione aritmetica finita?

Secondo la proprietà caratteristica, le espressioni date devono soddisfare la relazione

5X – 4 = ((3X + 2) + (11X + 12))/2.

Risolvendo questa equazione si ottiene X= –5,5. A questo valore X espressioni date 3 X + 2, 5X– 4 e 11 X+12 assumono rispettivamente i valori –14,5, –31,5, –48,5. Questa è una progressione aritmetica, la sua differenza è –17.

Progressione geometrica.

Una sequenza numerica, i cui termini sono tutti diversi da zero e ciascuno dei cui termini, a partire dal secondo, si ottiene dal termine precedente moltiplicando per lo stesso numero Q, è chiamata progressione geometrica e il numero Q- il denominatore di una progressione geometrica.

Pertanto, una progressione geometrica è una sequenza numerica ( b n), definita ricorsivamente dalle relazioni

B 1 = B, b n = b n –1 Q (N = 2, 3, 4…).

(B E Q - dati i numeri, B ≠ 0, Q ≠ 0).

Esempio 1. 2, 6, 18, 54, ... – progressione geometrica crescente B = 2, Q = 3.

Esempio 2. 2, –2, 2, –2, … – progressione geometrica B= 2,Q= –1.

Esempio 3. 8, 8, 8, 8, … – progressione geometrica B= 8, Q= 1.

Una progressione geometrica è una sequenza crescente se B 1 > 0, Q> 1 e decrescente se B 1 > 0, 0q

Una delle proprietà ovvie di una progressione geometrica è che se la sequenza è una progressione geometrica, allora lo è anche la sequenza di quadrati, cioè

B 1 2 , B 2 2 , B 3 2 , …, b n 2,... è una progressione geometrica il cui primo termine è uguale a B 1 2 , e il denominatore è Q 2 .

Formula N- l'esimo termine della progressione geometrica ha la forma

b n= B 1 qn– 1 .

È possibile ottenere una formula per la somma dei termini di una progressione geometrica finita.

Sia data una progressione geometrica finita

B 1 ,B 2 ,B 3 , …, b n

permettere Sn- la somma dei suoi membri, cioè

S n= B 1 + B 2 + B 3 + … +b n.

Questo è accettato Q N. 1. Determinare S n viene utilizzata una tecnica artificiale: vengono eseguite alcune trasformazioni geometriche dell'espressione Snq.

Snq = (B 1 + B 2 + B 3 + … + b n –1 + b n)Q = B 2 + B 3 + B 4 + …+ b n+ bnq = S n+ bnq– B 1 .

Così, Snq= S n +bnq – b 1 e quindi

Questa è la formula con umma n termini di progressione geometrica per il caso in cui Q≠ 1.

A Q= 1 non è necessario derivare la formula separatamente; è ovvio che in questo caso S n= UN 1 N.

La progressione è detta geometrica perché ogni termine in essa contenuto, tranne il primo, è uguale alla media geometrica dei termini precedente e successivo. Infatti, da allora

bn=bn- 1 Q;

bn = bn+ 1 /Q,

quindi, b n 2=bn– 1 miliardi+ 1 e vale il seguente teorema (proprietà caratteristica di una progressione geometrica):

una sequenza numerica è una progressione geometrica se e solo se il quadrato di ciascuno dei suoi termini, escluso il primo (e l'ultimo nel caso di sequenza finita), è uguale al prodotto dei termini precedente e successivo.

Limite di coerenza.

Sia una sequenza ( c n} = {1/N}. Questa successione è detta armonica, poiché ciascuno dei suoi termini, a partire dal secondo, è la media armonica tra il termine precedente e quello successivo. Media geometrica dei numeri UN E B c'è un numero

Altrimenti la successione si dice divergente.

Sulla base di questa definizione si può, ad esempio, dimostrare l'esistenza di un limite A=0 per la sequenza armonica ( c n} = {1/N). Sia ε un numero positivo arbitrariamente piccolo. Si considera la differenza

Esiste una cosa del genere? Nè per tutti n≥ N vale la disuguaglianza 1 /N ? Se lo prendiamo come N qualsiasi numero naturale maggiore di 1/ε , quindi per tutti n ≥ N vale la disuguaglianza 1 /n ≤ 1/Nε , Q.E.D.

Dimostrare la presenza di un limite per una particolare sequenza a volte può essere molto difficile. Le sequenze più frequenti sono ben studiate e sono elencate nei libri di consultazione. Esistono teoremi importanti che consentono di concludere che una determinata sequenza ha un limite (e persino di calcolarlo), sulla base di sequenze già studiate.

Teorema 1. Se una successione ha un limite, allora è limitata.

Teorema 2. Se una successione è monotona e limitata, allora ha un limite.

Teorema 3. Se la sequenza ( UN} ha un limite UN, quindi le sequenze ( Potere}, {UN+c) e (| UN|} avere dei limiti circa, UN +C, |UN| di conseguenza (qui C– numero arbitrario).

Teorema 4. Se le successioni ( UN} E ( b n) hanno limiti pari a UN E B padella + qbn) ha un limite papà+ qB.

Teorema 5. Se le successioni ( UN) E ( b n)hanno limiti pari a UN E B di conseguenza, allora la sequenza ( a n b n) ha un limite AB.

Teorema 6. Se le successioni ( UN} E ( b n) hanno limiti pari a UN E B di conseguenza e, inoltre, b n ≠ 0 e B≠ 0, quindi la sequenza ( un n/b n) ha un limite A/B.

Anna Chugainova

Argomento: sequenza numerica e modi per impostarla

Scopi principali e obiettivi della lezione
Didattico: spiegare agli studenti il ​​significato della sequenza di concetti, n-esimo membro della sequenza; introdurre metodi per impostare una sequenza.
Sviluppo: sviluppo dell'indipendenza, assistenza reciproca quando si lavora in gruppo, intelligenza.
Educativo: promuovere l'attività e l'accuratezza, la capacità di vedere sempre il bene, instillare amore e interesse per l'argomento

Risultati attesi dalla padronanza dell'argomento
Durante la lezione acquisiranno nuove conoscenze sulle sequenze numeriche e su come assegnarle. Impareranno a trovare la soluzione giusta, a creare un algoritmo risolutivo e ad usarlo per risolvere i problemi. Attraverso la ricerca si scopriranno alcune delle loro proprietà. Tutto il lavoro è accompagnato da diapositive.
Attività educative universali, la cui formazione è mirata nel processo educativo: capacità di lavorare in gruppo, sviluppare il pensiero logico, capacità di analizzare, ricercare, trarre conclusioni e difendere il proprio punto di vista. Insegnare abilità di comunicazione e collaborazione. L’uso di queste tecnologie contribuisce allo sviluppo dei metodi universali di attività, esperienza creativa, competenza e capacità di comunicazione degli studenti.

Idee chiave della lezione
Nuovi approcci all’insegnamento e all’apprendimento
- formazione al dialogo
- imparare ad imparare
Valutazione dell'apprendimento e valutazione dell'apprendimento
Insegnare il pensiero critico
Educazione di bambini talentuosi e dotati

Tipo di lezione
Imparare un nuovo argomento

Metodi di insegnamento
Visivo (presentazione), verbale (conversazione, spiegazione, dialogo), pratico.

Forme di organizzazione delle attività educative degli studenti
frontale; gruppo; bagno turco; individuale.

Metodi didattici interattivi utilizzati
Valutazione tra pari, Autovalutazione, Lavoro di gruppo, Lavoro individuale,
Valutazioni per l'apprendimento, ICT, Apprendimento differenziato

Applicazione dei moduli
Insegnare come apprendere, Insegnare il pensiero critico, Valutazioni per l'apprendimento, Usare le TIC nell'insegnamento e nell'apprendimento, Insegnare a bambini talentuosi e dotati

Attrezzature e materiali
Libro di testo, lavagna interattiva, lavagna luminosa, presentazione, pennarelli, wattmat A3, righello, matite colorate, adesivi, emoticon

Passi della lezione
DURANTE LE LEZIONI

Risultati previsti

Creazione di un ambiente collaborativo
Organizzare il tempo
(Accoglienza degli studenti, identificazione degli assenti, verifica della preparazione degli studenti per la lezione, organizzazione dell’attenzione).
Divisione in gruppi.
Discorso di apertura dell'insegnante
Parabola “Tutto è nelle tue mani”
C'era una volta, in una città, viveva un grande saggio. La fama della sua saggezza si diffuse in tutta la sua città natale, persone da lontano venivano da lui per chiedere consiglio. Ma c'era un uomo in città che era geloso della sua gloria. Una volta venne in un prato, catturò una farfalla, la piantò tra i suoi palmi chiusi e pensò: “Lasciami andare dal saggio e chiedergli: dimmi, o più saggio, quale farfalla è nelle mie mani: viva o morta? Se dice morto, aprirò i palmi delle mani, la farfalla volerà via, se dice vivo, chiuderò i palmi delle mani e la farfalla morirà. Allora tutti capiranno chi di noi è più intelligente”. È così che è successo tutto. Un uomo invidioso venne in città e chiese al saggio: "Dimmi, oh saggio, quale farfalla è nelle mie mani - viva o morta?" Allora il saggio, che era un uomo davvero intelligente, disse: "Tutto è nelle tue mani". mani."
Piena disponibilità dell'aula e dell'attrezzatura didattica per il lavoro; integrare rapidamente la classe nel ritmo aziendale, organizzando l'attenzione di tutti gli studenti

Lo scopo della lezione e gli obiettivi formativi della lezione saranno formulati in modo chiaro ed inequivocabile insieme agli studenti.

Parte principale della lezione
Preparare gli studenti ad un apprendimento attivo e consapevole.
Quali eventi nella nostra vita accadono in sequenza? Fornire esempi di tali fenomeni ed eventi.

Risposte degli studenti:
giorni della settimana,
nomi di mesi,
l'età della persona,
numero di conto bancario,
c'è un successivo cambiamento del giorno e della notte,
l'auto accelera in sequenza, le case sulla strada sono numerate in sequenza, ecc.

Compito per i gruppi:
Lavoro in gruppo, approccio differenziato
Ogni gruppo riceve il proprio compito. Dopo averlo completato, ogni gruppo si presenta alla classe, iniziano gli studenti del gruppo 1.

Compito per i gruppi:
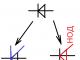
Agli studenti viene chiesto di trovare modelli e mostrarli con una freccia.

Compito per gli studenti dei gruppi 1 e 2:
1° gruppo:
In ordine crescente, numeri dispari positivi
1/2; 1/3; 1/4; 1/5; 1/6

In ordine decrescente le frazioni proprie con numeratore uguale a 1
5; 10; 15; 20; 25;

In ordine crescente, i numeri positivi multipli di 5
1; 3; 5; 7; 9;

Gruppo 2: trova modelli
6; 8; 16; 18; 36;
Aumenta di 3

10; 19; 37; 73; 145;
Ingrandimento alternativo di 2 e ingrandimento di 2 volte

1; 4; 7; 10; 13;
Aumenta di 2 volte e diminuisci di 1

Risposte del gruppo 1:
In ordine crescente, numeri dispari positivi (1; 3; 5; 7; 9;)
In ordine decrescente, le frazioni proprie con numeratore uguale a 1 (1/2; 1/3; 1/4; 1/5; 1/6)
In ordine crescente, i numeri positivi multipli di 5 (5; 10; 15; 20; 25;)

Risposte di 2 gruppi:
1; 4; 7; 10; 13; (Aumenta di 3)
10; 19; 37; 73; 145; (Aumenta di 2 e diminuisce di 1)
6; 8; 16; 18; 36; (Ingrandimento 2x alternativo e ingrandimento 2x)
Imparare nuovo materiale
- Cosa intendi anche con questa parola?
- Dare un esempio?
- Ora pronuncia diversi numeri pari di seguito
- Adesso ci parli dei numeri dispari?
- nominare numeri consecutivi non pari
BEN FATTO!
I numeri che compongono una sequenza si chiamano rispettivamente primo, secondo, terzo, ecc., n-esimi termini della sequenza.
I membri della sequenza sono designati come segue:
a1; a2; a3; a4; un;
Le sequenze possono essere finite o infinite, crescenti o decrescenti.

Lavorando su una lavagna a fogli mobili
xn=3n+2, quindi
x5=3,5+2=17;
x45=3,45+2=137.
Metodo ricorrente
Una formula che esprime qualsiasi membro della sequenza, a partire da alcuni, attraverso i precedenti (uno o più), è detta ricorrente (dal latino recurro - ritorno).
Ad esempio, la sequenza specificata dalla regola
a1=1; an+1= an +3
può essere scritto con i puntini di sospensione:
1; 4; 7; 10; 13;

Preparazione fisica 1,2,3,4,5,6,7, ...

4. Consolidamento del materiale studiato (lavoro in coppia, approccio differenziato)
Ogni gruppo riceve un compito individuale che completa in modo indipendente. Quando completano le attività, i bambini discutono la soluzione e la scrivono su un quaderno.

Sequenze date:
an=n4; an=(-1)nn2 ; an=n +4; an=-n-4; an=2n -5; an=3n -1.
Compito per gli studenti del gruppo 1: le sequenze sono date da formule. Inserisci i membri mancanti della sequenza:
1; ___; 81; ___; 625; ...
-1; 4; ___; ___; -25;
5; ___; ___; ___; 9;
___; -6; ___; ___ ; -9;
___; ___; 3; 11; ___;
2; 8; ___; ___; ___;
Esercizio:
Scrivi i primi cinque termini della sequenza data dalla formula del suo ennesimo termine.
Compito per gli studenti del gruppo:
Determina quali numeri sono i membri di queste sequenze e compila la tabella.

Numeri positivi e negativi

Numeri positivi

Numeri negativi

Lavorare con i libri di testo n. 148, n. 151

Lavoro di verifica
1. La sequenza è data dalla formula an=5n+2. A quanto vale il suo terzo termine?
a) 3 b) 17 c) 12 d) 22
2. Scrivi i primi 5 termini della sequenza data dalla formula an=n-3
a) -3,-2,-1,0,1 b) -2,-1,0,1,2
c) 0,-2,-4,-16,-50 d) 1,2,3,4,5

3. Trova la somma dei primi 6 termini della sequenza numerica: 2,4,6,8,
a) 66 b) 36 c) 32 d) 42
4. Quale delle seguenti sequenze è infinitamente decrescente:
a) b) 2,4,6,8,
CD)

Risposte: 1) b 2) b 3) d 4) d

Comunicazione dal vivo con l'insegnante

Gli studenti trovano le risposte alle domande poste.

Gli studenti imparano ad analizzare e trarre conclusioni.

La conoscenza si forma su come risolvere un sistema di diseguaglianze con una variabile

Risposte corrette nel processo di dialogo, comunicazione, attività degli studenti

Gli studenti completano il compito

Risolvi da solo, controlla le diapositive.
Non avranno paura degli errori; tutto diventerà chiaro sulle diapositive.

www. Bilimland.kz

Gli studenti conferiscono, lavorano in gruppo, si consultano con l'insegnante, i bambini dotati

Gli studenti nel lavoro in coppia si confrontano e trovano le soluzioni corrette al compito.

Gli studenti valutano il lavoro di un altro gruppo e danno un voto. I risultati mostrano che il materiale studiato è stato padroneggiato.
L'attività riproduttiva di uno studente è, prima di tutto, l'attività di uno studente che si riproduce secondo un determinato algoritmo, che porta al risultato richiesto.

Riflessione
Riassumendo
Quindi, abbiamo esaminato il concetto di sequenza e come definirlo.
Fornisci esempi di una sequenza numerica: finita e infinita.
Quali metodi di impostazione di una sequenza conosci?
Quale formula si chiama ricorrente?

Riassumi la lezione e annota gli studenti più attivi. Ringraziare gli studenti per il loro lavoro in classe.
Gli studenti attaccano appunti su adesivi,
su ciò che hanno imparato
cosa hanno imparato di nuovo?
come hai capito la lezione?
ti è piaciuta la lezione?
come si sono sentiti durante la lezione.

Compiti a casa.
9 №150, №152

Risposte corrette durante il dialogo, attività dello studente

Non ci saranno difficoltà quando si fanno i compiti

Regione di Atyrau
Distretto di Indersky
Villaggio di Esbol
scuola intitolata a Zhambyl
insegnante di matematica
categoria più alta,
insegnante certificato
Ho livello avanzato
Iskakova Svetlana Slambekovna

Obiettivo di apprendimento: fornire il concetto e la definizione di sequenza numerica, considerare modi per assegnare sequenze numeriche, risolvere esercizi.

Obiettivo evolutivo: sviluppare il pensiero logico, le capacità cognitive, le tecniche di calcolo, la capacità di confronto nella scelta delle formule, le capacità di lavoro accademico

Scopo educativo: promuovere motivazioni positive per l’apprendimento, un atteggiamento coscienzioso verso il lavoro e la disciplina.

Tipo di lezione: lezione sul fissaggio dei materiali.

Attrezzatura: lavagna interattiva, installazione di prova ACTIVwote, ACTIVwand, ACTIVslate, dispense.

Piano di lezione

1. Organizzazione delle lezioni.
2. Ripetizione di materiale teorico. Rilievo frontale. Riferimento storico.
3. Consolidamento: risoluzione di esercizi sull'argomento "Modi per assegnare sequenze numeriche".
4. Verifica delle conoscenze. Test
5. Compiti a casa.

Durante le lezioni

IO. Organizzare il tempo.

II. Ripetizione di materiale teorico.

1) Rilievo frontale.

1. Come si chiama una sequenza numerica?

Risposta: Un insieme di numeri i cui elementi possono essere numerati.

2. Fornisci un esempio di sequenza numerica.

Risposta:

2,4,6,8,10,…..
1,3,5,7,9,11,…..
3,6,9,12,15,….

3. Come vengono chiamati i membri di una sequenza numerica?

Risposta: Numeri che compongono una sequenza numerica.

un 1 =2, un 2 =4, un 3 =6 e 4 =8,….
a 1 = 1, a 2 = 3, a 3 = 5 e 4 = 7,….
a 1 = 3, a 2 = 6, a 3 = 9 e 4 = 12,….

4. Qual è un membro comune di una sequenza numerica?

Risposta: an è chiamato il membro generale della sequenza, e la sequenza stessa è brevemente denotata da (an).

5. Come si designa una sequenza numerica?

Risposta: Di solito una sequenza numerica è denotata da lettere minuscole dell'alfabeto latino con indici che indicano il numero di questo membro nella sequenza: a 1, a 2, a 3, a 4,…., a p,…

5. Quando una sequenza numerica è considerata data?

Risposta: Se possiamo specificare qualsiasi membro della sequenza.

2) Informazioni storiche.

Secondo il matematico Leibniz “chi vuole limitarsi al presente senza conoscere il passato non lo capirà mai”.

FIBONACCI (Leonardo da Pisa)

Fibonacci (Leonardo da Pisa),OK. 1175–1250

Matematico italiano. Nato a Pisa, divenne il primo grande matematico d'Europa nel tardo Medioevo. È stato attratto dalla matematica dalla necessità pratica di stabilire contatti d'affari. Ha pubblicato i suoi libri sull'aritmetica, l'algebra e altre discipline matematiche. Dai matematici musulmani apprese del sistema numerico inventato in India e già adottato nel mondo arabo, e si convinse della sua superiorità (questi numeri erano i predecessori dei moderni numeri arabi).

Leonardo da Pisa, noto come Fibonacci, fu il primo dei grandi matematici europei del tardo Medioevo. Nato a Pisa da una ricca famiglia di mercanti, si avvicinò alla matematica per un'esigenza puramente pratica di stabilire contatti d'affari. Nella sua giovinezza Leonardo viaggiò molto, accompagnando il padre in viaggi d'affari. Sappiamo, ad esempio, del suo lungo soggiorno a Bisanzio e in Sicilia. Durante tali viaggi, ha comunicato molto con gli scienziati locali.

La serie numerica che oggi porta il suo nome nasce dal problema del coniglio che Fibonacci descrisse nel suo libro Liber abacci, scritto nel 1202:

Un uomo mise una coppia di conigli in un recinto circondato su tutti i lati da un muro. Quante coppie di conigli può produrre questa coppia in un anno, se si sa che ogni mese, a partire dal secondo, ogni coppia di conigli produce una coppia?

Puoi star certo che il numero di coppie in ciascuno dei dodici mesi successivi sarà 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

In altre parole, il numero di coppie di conigli crea una serie, in cui ciascun termine è la somma dei due precedenti. È conosciuto come Serie di Fibonacci, e i numeri stessi - Numeri di Fibonacci. Si scopre che questa sequenza ha molte proprietà interessanti da un punto di vista matematico. Ecco un esempio: puoi dividere una linea in due segmenti, in modo che il rapporto tra il segmento più grande e quello più piccolo sia proporzionale al rapporto tra l'intera linea e il segmento più grande. Questo fattore di proporzionalità, circa 1.618, è noto come rapporto aureo. Durante il Rinascimento si credeva che fosse proprio questa proporzione, osservata nelle strutture architettoniche, a risultare più gradevole alla vista. Se prendi coppie successive dalla serie di Fibonacci e dividi il numero più grande di ciascuna coppia per il numero più piccolo, il tuo risultato si avvicinerà gradualmente alla sezione aurea.

Da quando Fibonacci scoprì la sua sequenza, sono stati riscontrati anche fenomeni naturali in cui questa sequenza sembra giocare un ruolo importante. Uno di loro - fillotassi(disposizione delle foglie) - la regola secondo la quale, ad esempio, i semi sono disposti in un'infiorescenza di girasole.I semi di girasole sono disposti in due spirali. I numeri che indicano il numero di semi in ciascuna spirale fanno parte di una sorprendente sequenza matematica.

I semi sono disposti su due file di spirali, una delle quali va in senso orario, l'altra in senso antiorario. E qual è il numero di semi in ciascun caso? 34 e 55.

Numeri di Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Una sequenza di numeri, ogni cui termine è uguale alla somma dei due precedenti, ha molte proprietà interessanti.

III.Consolidamento.

Lavora secondo il libro di testo (catena)

№343 Scrivi i primi cinque termini della sequenza.

1. un n =2 n +1/2 n

2.xn =3n2+2n+1

3.

1. Soluzione:

e n =2 n +1/2 n

Risposta:

2. Soluzione:

n=1,x1 =3*12 +2*1+1=3+2+1=6

n=2, x2 =3*2 2 +2*2+1=3*4+4+1=12+5=17

n=3, x3 =3*3 2 +2*3+1=27+6+1=34

n=4, x4 =3*4 2 +2-4+1=3*16+8+1=48+9=57

n=5, x5 =3*5 2 +2*5+1=3*25+10+1=75+11=86

Risposta: 6,17,34,57,86…….

3. Soluzione:

Risposta:

N. 344. Scrivi una formula per il termine comune di una sequenza di numeri naturali multipli di 3.

Risposta: 0,3,6,9,12,15,.... 3n, en =3n

N. 345. Scrivi una formula per il termine comune di una sequenza di numeri naturali multipli di 7.

Risposta: 0,7,14,25,28,35,42.... 7n, en =7n

N. 346 Scrivi una formula per il termine generale di una sequenza di numeri naturali che, divisa per 4, lasci come resto 1.

Risposta:5,9,13,17,21....... 4 n +1 e n =4n+1

N. 347 Scrivi una formula per il termine generale di una sequenza di numeri naturali che, divisa per 5, lasci come resto 2.

Risposta: a n =5n+2, 7.12,17,22, 27,.... 5 n +2

N. 348 Scrivi la formula per il termine generale della successione.

Vita sì= F(X), X DI N, Dove N– un insieme di numeri naturali (o una funzione di un argomento naturale), denotato sì=F(N) O sì 1 ,sì 2 ,…, sì, no,…. Valori sì 1 ,sì 2 ,sì 3 ,… sono chiamati rispettivamente primo, secondo, terzo, ... membri della sequenza.

Ad esempio, per la funzione sì= N 2 si può scrivere:

sì 1 = 1 2 = 1;

sì 2 = 2 2 = 4;

sì 3 = 3 2 = 9;…y n = n 2 ;…

Metodi per specificare le sequenze. Le sequenze possono essere specificate in vari modi, tra i quali tre sono particolarmente importanti: analitico, descrittivo e ricorrente.

1. Una successione è data analiticamente se viene data la sua formula N° membro:

sì, no=F(N).

Esempio. sì, no= 2N - 1 – sequenza di numeri dispari: 1, 3, 5, 7, 9, …

2. Descrittivo Il modo per specificare una sequenza numerica è spiegare da quali elementi è costruita la sequenza.

Esempio 1. "Tutti i termini della sequenza sono uguali a 1." Ciò significa che stiamo parlando di una sequenza stazionaria 1, 1, 1, …, 1, ….

Esempio 2: "La sequenza è composta da tutti i numeri primi in ordine crescente." Pertanto, la sequenza data è 2, 3, 5, 7, 11, …. Con questo metodo di specificazione della sequenza in questo esempio, è difficile rispondere a cosa, ad esempio, è uguale il millesimo elemento della sequenza.

3. Il metodo ricorrente per specificare una sequenza consiste nel specificare una regola che consenta di eseguire il calcolo N-esimo membro di una sequenza se i suoi membri precedenti sono noti. Il nome metodo ricorrente deriva dalla parola latina ricorrente- ritorno. Molto spesso, in questi casi, viene indicata una formula che consente di esprimere N dall'esimo membro della sequenza fino ai precedenti e specificare 1–2 membri iniziali della sequenza.

Esempio 1. sì 1 = 3; sì n = sì n–1 + 4 se N = 2, 3, 4,….

Qui sì 1 = 3; sì 2 = 3 + 4 = 7;sì 3 = 7 + 4 = 11; ….

Come puoi vedere, la sequenza ottenuta in questo esempio può essere specificata anche analiticamente: sì, no= 4N - 1.

Esempio 2. sì 1 = 1; sì 2 = 1; sì, no = sì, no –2 + sì, no–1 se N = 3, 4,….

Qui: sì 1 = 1; sì 2 = 1; sì 3 = 1 + 1 = 2; sì 4 = 1 + 2 = 3; sì 5 = 2 + 3 = 5; sì 6 = 3 + 5 = 8;

La sequenza in questo esempio è studiata soprattutto in matematica perché ha una serie di proprietà e applicazioni interessanti. Si chiama sequenza di Fibonacci, dal nome del matematico italiano del XIII secolo. È molto facile definire la sequenza di Fibonacci in modo ricorrente, ma molto difficile analiticamente. N L'esimo numero di Fibonacci si esprime attraverso il suo numero seriale mediante la seguente formula.

A prima vista, la formula per N l'esimo numero di Fibonacci sembra poco plausibile, poiché la formula che specifica la sequenza dei numeri naturali contiene solo radici quadrate, ma è possibile verificare “manualmente” la validità di questa formula per i primi N.

Proprietà delle sequenze numeriche.

Una sequenza numerica è un caso speciale di una funzione numerica, pertanto per le sequenze vengono considerate anche alcune proprietà delle funzioni.

Definizione . Sotto sequenza ( sì, no} si dice crescente se ciascuno dei suoi termini (eccetto il primo) è maggiore del precedente:

sì 1 sì 2 sì 3 sì no sì n +1

Definizione.Sequenza ( sì, no} si dice decrescente se ciascuno dei suoi termini (eccetto il primo) è minore del precedente:

sì 1 > sì 2 > sì 3 > … > sì, no> sì, no +1 > … .

Le sequenze crescenti e decrescenti sono combinate sotto il termine comune: sequenze monotone.

Esempio 1. sì 1 = 1; sì, no= N 2 – sequenza crescente.

Pertanto è vero il seguente teorema (una proprietà caratteristica di una progressione aritmetica). Una sequenza numerica è aritmetica se e solo se ciascuno dei suoi membri, tranne il primo (e l'ultimo nel caso di una sequenza finita), è uguale alla media aritmetica dei membri precedenti e successivi.

Esempio. A quale valore X numeri 3 X + 2, 5X– 4 e 11 X+ 12 formano una progressione aritmetica finita?

Secondo la proprietà caratteristica, le espressioni date devono soddisfare la relazione

5X – 4 = ((3X + 2) + (11X + 12))/2.

Risolvendo questa equazione si ottiene X= –5,5. A questo valore X espressioni date 3 X + 2, 5X– 4 e 11 X+12 assumono rispettivamente i valori –14,5, –31,5, –48,5. Questa è una progressione aritmetica, la sua differenza è –17.

Progressione geometrica.

Una sequenza numerica, i cui termini sono tutti diversi da zero e ciascuno dei cui termini, a partire dal secondo, si ottiene dal termine precedente moltiplicando per lo stesso numero Q, è chiamata progressione geometrica e il numero Q- il denominatore di una progressione geometrica.

Pertanto, una progressione geometrica è una sequenza numerica ( b n), definita ricorsivamente dalle relazioni

B 1 = B, b n = b n –1 Q (N = 2, 3, 4…).

(B E Q - dati i numeri, B ≠ 0, Q ≠ 0).

Esempio 1. 2, 6, 18, 54, ... – progressione geometrica crescente B = 2, Q = 3.

Esempio 2. 2, –2, 2, –2, … – progressione geometrica B= 2,Q= –1.

Esempio 3. 8, 8, 8, 8, … – progressione geometrica B= 8, Q= 1.

Una progressione geometrica è una sequenza crescente se B 1 > 0, Q> 1 e decrescente se B 1 > 0, 0q

Una delle proprietà ovvie di una progressione geometrica è che se la sequenza è una progressione geometrica, allora lo è anche la sequenza di quadrati, cioè

B 1 2 , B 2 2 , B 3 2 , …, b n 2,... è una progressione geometrica il cui primo termine è uguale a B 1 2 , e il denominatore è Q 2 .

Formula N- l'esimo termine della progressione geometrica ha la forma

b n= B 1 qn– 1 .

È possibile ottenere una formula per la somma dei termini di una progressione geometrica finita.

Sia data una progressione geometrica finita

B 1 ,B 2 ,B 3 , …, b n

permettere Sn- la somma dei suoi membri, cioè

S n= B 1 + B 2 + B 3 + … +b n.

Questo è accettato Q N. 1. Determinare S n viene utilizzata una tecnica artificiale: vengono eseguite alcune trasformazioni geometriche dell'espressione Snq.

Snq = (B 1 + B 2 + B 3 + … + b n –1 + b n)Q = B 2 + B 3 + B 4 + …+ b n+ bnq = S n+ bnq– B 1 .

Così, Snq= S n +bnq – b 1 e quindi

Questa è la formula con umma n termini di progressione geometrica per il caso in cui Q≠ 1.

A Q= 1 non è necessario derivare la formula separatamente; è ovvio che in questo caso S n= UN 1 N.

La progressione è detta geometrica perché ogni termine in essa contenuto, tranne il primo, è uguale alla media geometrica dei termini precedente e successivo. Infatti, da allora

bn=bn- 1 Q;

bn = bn+ 1 /Q,

quindi, b n 2=bn– 1 miliardi+ 1 e vale il seguente teorema (proprietà caratteristica di una progressione geometrica):

una sequenza numerica è una progressione geometrica se e solo se il quadrato di ciascuno dei suoi termini, escluso il primo (e l'ultimo nel caso di sequenza finita), è uguale al prodotto dei termini precedente e successivo.

Limite di coerenza.

Sia una sequenza ( c n} = {1/N}. Questa successione è detta armonica, poiché ciascuno dei suoi termini, a partire dal secondo, è la media armonica tra il termine precedente e quello successivo. Media geometrica dei numeri UN E B c'è un numero

Altrimenti la successione si dice divergente.

Sulla base di questa definizione si può, ad esempio, dimostrare l'esistenza di un limite A=0 per la sequenza armonica ( c n} = {1/N). Sia ε un numero positivo arbitrariamente piccolo. Si considera la differenza

Esiste una cosa del genere? Nè per tutti n≥ N vale la disuguaglianza 1 /N ? Se lo prendiamo come N qualsiasi numero naturale maggiore di 1/ε , quindi per tutti n ≥ N vale la disuguaglianza 1 /n ≤ 1/Nε , Q.E.D.

Dimostrare la presenza di un limite per una particolare sequenza a volte può essere molto difficile. Le sequenze più frequenti sono ben studiate e sono elencate nei libri di consultazione. Esistono teoremi importanti che consentono di concludere che una determinata sequenza ha un limite (e persino di calcolarlo), sulla base di sequenze già studiate.

Teorema 1. Se una successione ha un limite, allora è limitata.

Teorema 2. Se una successione è monotona e limitata, allora ha un limite.

Teorema 3. Se la sequenza ( UN} ha un limite UN, quindi le sequenze ( Potere}, {UN+c) e (| UN|} avere dei limiti circa, UN +C, |UN| di conseguenza (qui C– numero arbitrario).

Teorema 4. Se le successioni ( UN} E ( b n) hanno limiti pari a UN E B padella + qbn) ha un limite papà+ qB.

Teorema 5. Se le successioni ( UN) E ( b n)hanno limiti pari a UN E B di conseguenza, allora la sequenza ( a n b n) ha un limite AB.

Teorema 6. Se le successioni ( UN} E ( b n) hanno limiti pari a UN E B di conseguenza e, inoltre, b n ≠ 0 e B≠ 0, quindi la sequenza ( un n/b n) ha un limite A/B.

Anna Chugainova