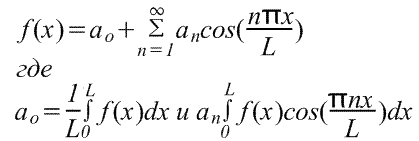Disporre in serie di Fourier all'intervallo indicato. Serie di Fourier. Esempi di soluzioni

Serie di Fourier di funzioni periodiche con periodo 2π.

La serie di Fourier permette di studiare le funzioni periodiche scomponendole in componenti. Correnti e tensioni alternate, spostamenti, velocità e accelerazione dei manovellismi e onde acustiche sono tipici esempi pratici dell'uso delle funzioni periodiche nei calcoli ingegneristici.

Lo sviluppo in serie di Fourier si basa sul presupposto che tutte le funzioni di significato pratico nell'intervallo -π ≤x≤ π possano essere espresse sotto forma di serie trigonometriche convergenti (una serie è considerata convergente se la successione di somme parziali composta dai suoi termini converge):

Notazione standard (=ordinaria) attraverso la somma di sinx e cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

dove a o, a 1,a 2,...,b 1,b 2,.. sono costanti reali, cioè

Dove, per l'intervallo da -π a π, i coefficienti della serie di Fourier si calcolano utilizzando le formule:

Si chiamano i coefficienti a o , a n e b n Coefficienti di Fourier, e se possono essere trovati, allora viene chiamata la serie (1). accanto a Fourier, corrispondente alla funzione f(x). Per la serie (1), il termine (a 1 cosx+b 1 sinx) è detto primo o armonica fondamentale,

Un altro modo per scrivere una serie è usare la relazione acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Dove a o è una costante, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 sono le ampiezze delle varie componenti, ed è uguale a a n =arctg a n /b n.

Per la serie (1), il termine (a 1 cosx+b 1 sinx) oppure c 1 sin(x+α 1) è detto primo o armonica fondamentale,(a 2 cos2x+b 2 sin2x) oppure c 2 sin(2x+α 2) si chiama seconda armonica e così via.

Per rappresentare accuratamente un segnale complesso è necessario in genere un numero infinito di termini. Tuttavia, in molti problemi pratici è sufficiente considerare solo i primi termini.

Serie di Fourier di funzioni non periodiche con periodo 2π.

Espansione di funzioni non periodiche.

Se la funzione f(x) è non periodica, significa che non può essere sviluppata in una serie di Fourier per tutti i valori di x. Tuttavia, è possibile definire una serie di Fourier che rappresenta una funzione su qualsiasi intervallo di larghezza 2π.

Data una funzione non periodica, è possibile costruire una nuova funzione selezionando valori di f(x) entro un certo intervallo e ripetendoli al di fuori di tale intervallo a intervalli di 2π. Poiché la nuova funzione è periodica con periodo 2π, può essere espansa in una serie di Fourier per tutti i valori di x. Ad esempio, la funzione f(x)=x non è periodica. Tuttavia, se è necessario espanderlo in una serie di Fourier nell'intervallo da o a 2π, allora al di fuori di questo intervallo viene costruita una funzione periodica con un periodo di 2π (come mostrato nella figura seguente).

Per funzioni non periodiche come f(x)=x, la somma della serie di Fourier è uguale al valore di f(x) in tutti i punti in un dato intervallo, ma non è uguale a f(x) per i punti fuori portata. Per trovare la serie di Fourier di una funzione non periodica nell'intervallo 2π, viene utilizzata la stessa formula dei coefficienti di Fourier.

Funzioni pari e dispari.

Dicono che la funzione y=f(x) Anche, se f(-x)=f(x) per tutti i valori di x. I grafici delle funzioni pari sono sempre simmetrici rispetto all'asse y (cioè sono immagini speculari). Due esempi di funzioni pari: y=x2 e y=cosx.

Dicono che la funzione y=f(x) strano, se f(-x)=-f(x) per tutti i valori di x. I grafici delle funzioni dispari sono sempre simmetrici rispetto all'origine.

Molte funzioni non sono né pari né dispari.

Espansione in serie di Fourier in coseni.

La serie di Fourier di una funzione periodica pari f(x) con periodo 2π contiene solo termini coseno (cioè nessun termine seno) e può includere un termine costante. Quindi,

dove sono i coefficienti della serie di Fourier,

La serie di Fourier di una funzione periodica dispari f(x) con periodo 2π contiene solo termini con seni (cioè non contiene termini con coseni).

Quindi,

dove sono i coefficienti della serie di Fourier,

Serie di Fourier a mezzo ciclo.

Se una funzione è definita per un intervallo, ad esempio da 0 a π, e non solo da 0 a 2π, può essere espansa in una serie solo in seni o solo in coseni. La serie di Fourier risultante viene chiamata vicino a Fourier a metà ciclo.

Se vuoi ottenere la scomposizione Mezzo ciclo di Fourier per coseni funzioni f(x) nell'intervallo da 0 a π, allora è necessario costruire una funzione periodica pari. Nella fig. Di seguito è riportata la funzione f(x)=x, costruita sull'intervallo da x=0 a x=π. Poiché la funzione pari è simmetrica rispetto all'asse f(x), tracciamo la linea AB, come mostrato in Fig. sotto. Se assumiamo che al di fuori dell'intervallo considerato la forma triangolare risultante sia periodica con periodo 2π, il grafico finale sarà simile a questo: nella fig. sotto. Poiché dobbiamo ottenere lo sviluppo di Fourier in coseni, come prima, calcoliamo i coefficienti di Fourier a o e a n

Se hai bisogno di ottenere Espansione del seno a semiciclo di Fourier funzioni f(x) nell'intervallo da 0 a π, allora è necessario costruire una funzione periodica dispari. Nella fig. Di seguito è riportata la funzione f(x)=x, costruita sull'intervallo da x=0 a x=π. Poiché la funzione dispari è simmetrica rispetto all'origine, costruiamo la retta CD, come mostrato in Fig. Se assumiamo che al di fuori dell’intervallo considerato il segnale a dente di sega risultante sia periodico con periodo 2π, allora il grafico finale avrà la forma mostrata in Fig. Poiché dobbiamo ottenere l'espansione di Fourier del semiciclo in termini di seno, come prima, calcoliamo il coefficiente di Fourier. B

Serie di Fourier per un intervallo arbitrario.

Sviluppo di una funzione periodica con periodo L.

La funzione periodica f(x) si ripete quando x aumenta di L, cioè f(x+L)=f(x). Il passaggio dalle funzioni con periodo 2π precedentemente considerate alle funzioni con periodo L è abbastanza semplice, poiché può essere effettuato mediante un cambio di variabile.

Per trovare la serie di Fourier della funzione f(x) nell'intervallo -L/2≤x≤L/2, introduciamo una nuova variabile u in modo che la funzione f(x) abbia un periodo di 2π rispetto a u. Se u=2πx/L, allora x=-L/2 per u=-π e x=L/2 per u=π. Sia anche f(x)=f(Lu/2π)=F(u). La serie di Fourier F(u) ha la forma

(I limiti di integrazione possono essere sostituiti da qualsiasi intervallo di lunghezza L, ad esempio da 0 a L)

Serie di Fourier su semiciclo per funzioni specificate nell'intervallo L≠2π.

Per la sostituzione u=πх/L, l'intervallo da x=0 a x=L corrisponde all'intervallo da u=0 a u=π. Di conseguenza la funzione può essere sviluppata in una serie solo in coseni o solo in seni, cioè V Serie di Fourier a mezzo ciclo.

L'espansione del coseno nell'intervallo da 0 a L ha la forma

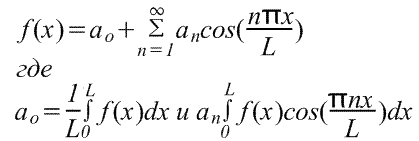
Espansione in serie di funzioni pari e dispari espansione di una funzione data su un intervallo in una serie in seni o coseni Serie di Fourier per una funzione con un periodo arbitrario Rappresentazione complessa della serie di Fourier Serie di Fourier in sistemi ortogonali generali di funzioni Serie di Fourier in un sistema ortogonale Proprietà minima dei coefficienti di Fourier Disuguaglianza di Bessel Uguaglianza Parseval Sistemi chiusi Completezza e chiusura dei sistemi

Espansione in serie di Fourier di funzioni pari e dispari Una funzione f(x), definita sull'intervallo \-1, dove I > 0, è detta anche se il grafico della funzione pari è simmetrico rispetto all'asse delle ordinate. Una funzione f(x), definita sul segmento J), dove I > 0, è detta dispari se il grafico della funzione dispari è simmetrico rispetto all'origine. Esempio. a) La funzione è pari sull'intervallo |-jt, jt), poiché per tutti gli x e b) La funzione è dispari, poiché l'espansione in serie di Fourier delle funzioni pari e dispari è l'espansione di una funzione data su un intervallo in una serie in seni o coseni Serie di Fourier per una funzione con un periodo arbitrario Rappresentazione complessa della serie di Fourier Serie di Fourier per sistemi di funzioni ortogonali generali Serie di Fourier per un sistema ortogonale Proprietà minima dei coefficienti di Fourier Disuguaglianza di Bessel Uguaglianza di Parseval Sistemi chiusi Completezza e chiusura dei sistemi c) Funzione f (x)=x2-x, dove non appartiene né alle funzioni pari né a quelle dispari, poiché sia ​​pari sull'intervallo x| la funzione f(x), che soddisfa le condizioni del Teorema 1. Quindi per tutti, ad es. /(x) cos nx è una funzione pari e f(x) sinnx è dispari. Pertanto, i coefficienti di Fourier di una funzione pari f(x) saranno uguali, pertanto la serie di Fourier di una funzione pari ha la forma f(x) sin х - una funzione pari. Pertanto, avremo Così, la serie di Fourier di una funzione dispari ha la forma Esempio 1. Espandi la funzione 4 in una serie di Fourier sull'intervallo -x ^ x ^ n Poiché questa funzione è pari e soddisfa le condizioni del Teorema 1, quindi la sua serie di Fourier ha la forma Trova i coefficienti di Fourier. Abbiamo Applicando due volte l'integrazione per parti, otteniamo che Quindi, la serie di Fourier di questa funzione si presenta così: oppure, in forma estesa, Questa uguaglianza è valida per qualsiasi x €, poiché nei punti x = ±ir la somma delle coincide con i valori della funzione f(x) = x2, poiché i grafici della funzione f(x) = x e la somma delle serie risultanti sono riportati in Fig. Commento. Questa serie di Fourier ci permette di trovare la somma di una delle serie numeriche convergenti, vale a dire, per x = 0 otteniamo l'Esempio 2. Espandi la funzione /(x) = x in una serie di Fourier sull'intervallo. La funzione /(x) soddisfa le condizioni del Teorema 1, quindi può essere sviluppata in una serie di Fourier, che, a causa della stranezza di questa funzione, avrà la forma Integrando per parti, troviamo i coefficienti di Fourier. La serie di Fourier di questa funzione ha la forma Questa uguaglianza vale per tutti gli x B nei punti x - ±t la somma della serie di Fourier non coincide con i valori della funzione /(x) = x, poiché è uguale a Al di fuori dell'intervallo [-*, i-] la somma della serie è una continuazione periodica della funzione /(x) = x; il suo grafico è mostrato in Fig. 6. § 6. Espansione di una funzione data su un intervallo in una serie in seni o coseni Sia data sull'intervallo una funzione monotona a tratti limitata /. I valori di questa funzione sull'intervallo 0| può essere ulteriormente definito in vari modi. Ad esempio, puoi definire una funzione / sul segmento tc] in modo che /. In questo caso si dice che) “si estende al segmento 0] in modo uniforme”; la sua serie di Fourier conterrà solo coseni. Se la funzione /(x) è definita sull’intervallo [-l-, mc] in modo che /(, allora il risultato è una funzione dispari, e quindi si dice che / è “esteso all’intervallo [-*, 0] in un modo strano"; in questo In questo caso, la serie di Fourier conterrà solo seni. Pertanto, ciascuna funzione monotona a tratti limitata /(x) definita sull'intervallo può essere espansa in una serie di Fourier sia in seno che in coseno. Esempio 1 Espandi la funzione in serie di Fourier: a) mediante i coseni; b) dai seni. M Questa funzione, con le sue continuazioni pari e dispari nel segmento |-x,0) sarà limitata e monotona a tratti. a) Estendi /(z) nel segmento 0) a) Estendi j\x) nel segmento (-π,0| in modo uniforme (Fig. 7), allora la sua serie di Fourier i avrà la forma Π = 1 dove i coefficienti di Fourier sono uguali, rispettivamente per Pertanto, b) Estendiamo /(z) nel segmento [-x,0] in modo dispari (Fig. 8). Quindi la sua serie di Fourier §7. Serie di Fourier per una funzione con un periodo arbitrario Sia la funzione fix) periodica con un periodo di 21,1 ^ 0. Per espanderla in una serie di Fourier sull'intervallo in cui I > 0, apportiamo un cambio di variabile ponendo x = jt . Allora la funzione F(t) = / ^tj sarà una funzione periodica dell'argomento t con periodo e potrà essere espansa sul segmento in una serie di Fourier. Ritornando alla variabile x, cioè impostando, otteniamo Tutti i teoremi validi per serie di Fourier di funzioni periodiche con periodo 2π , restano validi per funzioni periodiche con periodo arbitrario 21. In particolare resta valido anche un criterio sufficiente per la scomponibilità di una funzione in una serie di Fourier. Esempio 1. Espandi in una serie di Fourier una funzione periodica con un periodo di 21, dato sull'intervallo [-/,/] dalla formula (Fig. 9). Poiché questa funzione è pari, la sua serie di Fourier ha la forma Sostituendo i valori trovati dei coefficienti di Fourier nella serie di Fourier, otteniamo Notiamo un'importante proprietà delle funzioni periodiche. Teorema 5. Se una funzione ha periodo T ed è integrabile, allora per qualsiasi numero a vale l'uguaglianza m. cioè, l'integrale di un segmento la cui lunghezza è uguale al periodo T ha lo stesso valore indipendentemente dalla posizione di questo segmento sull'asse dei numeri. Infatti, facciamo un cambio di variabile nel secondo integrale, assumendo. Ciò dà e quindi, geometricamente, questa proprietà fa sì che nel caso della zona ombreggiata in Fig. 10 aree sono uguali tra loro. In particolare, per una funzione f(x) con periodo si ottiene a Espansione in una serie di Fourier di funzioni pari e dispari, espansione di una funzione data su un intervallo in una serie di seni o coseni Serie di Fourier per una funzione con periodo arbitrario periodo Notazione complessa della serie di Fourier Serie di Fourier in generale sistemi ortogonali funzioni Serie di Fourier in un sistema ortogonale Proprietà minima dei coefficienti di Fourier Disuguaglianza di Bessel Uguaglianza di Parseval Sistemi chiusi Completezza e chiusura dei sistemi Esempio 2. La funzione x è periodica con un periodo A causa della stranezza di questa funzione, senza calcolare integrali, possiamo affermare che per qualsiasi La proprietà provata, in particolare, mostra che i coefficienti di Fourier di una funzione periodica f(x) con periodo 21 possono essere calcolati utilizzando le formule dove a è un numero reale arbitrario (notare che le funzioni cos - e sin hanno un periodo di 2/). Esempio 3. Espandi in una serie di Fourier una funzione data su un intervallo con un periodo di 2x (Fig. 11). 4 Troviamo i coefficienti di Fourier di questa funzione. Inserendo le formule troviamo che per Pertanto la serie di Fourier sarà così: Nel punto x = jt (punto di discontinuità della prima specie) abbiamo §8. Registrazione complessa della serie di Fourier Questa sezione utilizza alcuni elementi di analisi complessa (vedi Capitolo XXX, dove tutte le azioni qui eseguite con espressioni complesse sono rigorosamente giustificate). Sia la funzione f(x) a soddisfare condizioni sufficienti per l'espansione in una serie di Fourier. Allora sul segmento x] può essere rappresentato da una serie della forma Usando le formule di Eulero Sostituendo queste espressioni nella serie (1) invece di cos πx e sin φx avremo Introduciamo la seguente notazione Allora la serie (2) prenderà la forma Pertanto, la serie di Fourier (1) è rappresentata in forma complessa (3). Troviamo le espressioni dei coefficienti tramite gli integrali. Abbiamo Allo stesso modo, troviamo Le formule finali per с„, с_п e с possono essere scritte come segue: . . I coefficienti с„ sono chiamati coefficienti complessi di Fourier della funzione. Per una funzione periodica con un periodo), la forma complessa della serie di Fourier assumerà la forma in cui i coefficienti Cn vengono calcolati utilizzando le formule. La convergenza delle serie (3 ) e (4) si intende come segue: le serie (3) e (4) si dicono convergenti per dati valori se esistono limiti Esempio. Espandi la funzione periodo in una serie di Fourier complessa. Questa funzione soddisfa condizioni sufficienti per l'espansione in una serie di Fourier. Troviamo i complessi coefficienti di Fourier di questa funzione. Abbiamo per dispari per pari n, o, in breve. Sostituendo i valori), otteniamo infine Notare che questa serie può anche essere scritta come segue: Serie di Fourier per sistemi di funzioni ortogonali generali 9.1. Sistemi ortogonali di funzioni Indichiamo con l'insieme di tutte le funzioni (reali) definite e integrabili sull'intervallo [a, 6] con un quadrato, cioè quelle per le quali esiste un integrale. In particolare, tutte le funzioni f(x) continue sull'intervallo [a, 6], appartengono a 6], e i valori dei loro integrali di Lebesgue coincidono con i valori degli integrali di Riemann. Definizione. Un sistema di funzioni, dove, si dice ortogonale sull'intervallo [a, b\, se la Condizione (1) presuppone, in particolare, che nessuna delle funzioni sia identicamente nulla. L'integrale è inteso nel senso di Lebesgue. e chiamiamo la quantità norma della funzione.Se in un sistema ortogonale per qualsiasi n abbiamo, allora il sistema di funzioni è chiamato ortonormale. Se il sistema (y>„(x)) è ortogonale, allora il sistema Esempio 1. Il sistema trigonometrico è ortogonale su un segmento. Il sistema di funzioni è un sistema di funzioni ortonormale, Esempio 2. Il sistema coseno e il sistema seno sono ortonormali. Introduciamo la notazione che sono ortogonali sull'intervallo (0, f|, ma non ortonormali (per I Ф- 2). Poiché le loro norme sono COS Esempio 3. I polinomi definiti dall'uguaglianza sono chiamati polinomi di Legendre (polinomi). n = 0 abbiamo Si può dimostrare che le funzioni formano un sistema ortonormale di funzioni sull'intervallo. Mostriamo, ad esempio, l'ortogonalità dei polinomi di Legendre. Sia m > n. In questo caso, integrando n volte per parti, troviamo poiché per la funzione t/m = (z2 - I)m tutte le derivate fino all'ordine m - I compreso si annullano agli estremi del segmento [-1,1). Definizione. Un sistema di funzioni (pn(x)) si dice ortogonale sull'intervallo (a, b) da uno sbalzo p(x) se: 1) per ogni n = 1,2,... esistono integrali. Eccolo si supponga che la funzione peso p(x) sia definita e positiva ovunque nell'intervallo (a, b) con la possibile eccezione di un numero finito di punti in cui p(x) può annullarsi. Dopo aver eseguito la differenziazione nella formula (3), troviamo. Si può dimostrare che i polinomi di Chebyshev-Hermite sono ortogonali sull'intervallo Esempio 4. Il sistema di funzioni di Bessel (jL(pix)^ è ortogonale sugli zeri dell'intervallo della funzione di Bessel Esempio 5. Consideriamo i polinomi di Chebyshev-Hermite, che può essere definita utilizzando l'uguaglianza Serie di Fourier sul sistema ortogonale Sia presente un sistema ortogonale di funzioni nell'intervallo (a, 6) e sia la serie (cj = const) a convergere su questo intervallo alla funzione f(x): Moltiplicando entrambi i membri dell'ultima uguaglianza per - fisso) e integrando su x da a a 6, in A causa dell'ortogonalità del sistema, otteniamo che questa operazione ha, in generale, un carattere puramente formale. Tuttavia in alcuni casi, ad esempio quando la serie (4) converge uniformemente, tutte le funzioni sono continue e l'intervallo (a, 6) è finito, questa operazione è legale. Ma per noi adesso ciò che conta è l’interpretazione formale. Sia data quindi una funzione. Formiamo i numeri c* secondo la formula (5) e scriviamo. La serie a destra si chiama serie di Fourier della funzione f(x) rispetto al sistema (^n(i)). I numeri Cn sono chiamati coefficienti di Fourier della funzione f(x) rispetto a questo sistema. Il segno ~ nella formula (6) significa solo che i numeri Cn sono legati alla funzione f(x) dalla formula (5) (non si assume che la serie a destra converga affatto, tanto meno che converga alla funzione f (X)). Pertanto, sorge spontanea la domanda: quali sono le proprietà di questa serie? In che senso “rappresenta” la funzione f(x)? 9.3. Convergenza in media Definizione. Una successione converge in media all'elemento ] se la norma è nello spazio Teorema 6. Se una successione ) converge uniformemente, allora converge in media. M Sia la successione ()) a convergere uniformemente sull'intervallo [a, b] alla funzione /(x). Ciò significa che per tutti, per tutti gli n sufficientemente grandi, abbiamo Pertanto, da cui segue la nostra affermazione. Non è vero il contrario: la successione () può convergere mediamente a /(x), ma non essere uniformemente convergente. Esempio. Considerando la successione nx, è facile vederlo Ma questa convergenza non è uniforme: esiste e, ad esempio, tale che, non importa quanto grande sia n, sull'intervallo coseni Serie di Fourier per una funzione con un periodo arbitrario Rappresentazione complessa della serie di Fourier Serie di Fourier per sistemi generali di funzioni ortogonali Serie di Fourier per un sistema ortogonale Proprietà minima dei coefficienti di Fourier Disuguaglianza di Bessel Uguaglianza di Parseval Sistemi chiusi Completezza e chiusura dei sistemi e indichiamo con c* i coefficienti di Fourier della funzione /(x ) da un sistema ortonormale b Considera una combinazione lineare in cui n^1 è un numero intero fisso, e trova i valori delle costanti in corrispondenza delle quali l'integrale assume un valore minimo. Scriviamolo più nel dettaglio: integrando termine per termine, a causa dell'ortonormalità del sistema, otteniamo che i primi due termini a destra dell'uguaglianza (7) sono indipendenti, e il terzo termine è non negativo. Pertanto, l'integrale (*) assume un valore minimo in ak = sk ed è chiamato approssimazione quadratica media della funzione /(x) mediante una combinazione lineare di Tn(x). Pertanto, l'approssimazione del valore quadratico medio della funzione /\ assume un valore minimo quando. quando Tn(x) è la 71esima somma parziale della serie di Fourier della funzione /(x) sul sistema (. Ponendo ak = sk, da (7) si ottiene L'uguaglianza (9) è chiamata identità di Bessel. Poiché è a sinistra lato non è negativo, da esso segue la disuguaglianza di Bessel. Poiché sono qui arbitrariamente, la disuguaglianza di Bessel può essere rappresentata in una forma rafforzata, cioè per qualsiasi funzione / la serie dei coefficienti di Fourier quadrati di questa funzione in un sistema ortonormale ) converge . Poiché il sistema è ortonormale sull'intervallo [-x, m], allora la disuguaglianza (10) tradotta nella consueta notazione della serie trigonometrica di Fourier dà la relazione do valida per qualsiasi funzione /(x) con un quadrato integrabile. Se f2(x) è integrabile, allora, per la condizione necessaria alla convergenza della serie sul membro sinistro della disuguaglianza (11), otteniamo che. Uguaglianza di Parseval Per alcuni sistemi (^„(x)), il segno di disuguaglianza nella formula (10) può essere sostituito (per tutte le funzioni f(x) 6 ×) con un segno di uguale. L'uguaglianza risultante è chiamata uguaglianza di Parseval-Steklov (condizione di completezza). L'identità di Bessel (9) ci permette di scrivere la condizione (12) in forma equivalente, pertanto il soddisfacimento della condizione di completezza fa sì che le somme parziali Sn(x) della serie di Fourier della funzione /(x) convergano alla funzione /(x) in media, cioè secondo la norma dello spazio 6]. Definizione. Un sistema ortonormale ( si dice completo in b2[аy b] se ogni funzione può essere approssimata mediamente con una certa accuratezza mediante una combinazione lineare della forma con un numero sufficientemente grande di termini, cioè se per qualsiasi funzione /(x) ∈ b2 [a, b\ e per ogni e > 0 esiste un numero naturale nq e numeri a\, a2y..., tali che No Dal ragionamento precedente segue il Teorema 7. Se per ortonormalizzazione il sistema ) è completo nello spazio, il La serie di Fourier di qualsiasi funzione / in questo sistema converge in media a f( x), cioè secondo la norma. Si può dimostrare che il sistema trigonometrico è completo nello spazio. Ciò implica l'affermazione. Teorema 8. Se una funzione /o la sua serie trigonometrica di Fourier converge ad essa in media. 9.5. Sistemi chiusi. Completezza e chiusura dei sistemi Definizione. Un sistema ortonormale di funzioni \ si dice chiuso se nello spazio Li\a, b) non esiste una funzione ortogonale a tutte le funzioni diversa da zero. Nello spazio L2\a, b\ i concetti di completezza e chiusura dei sistemi ortonormali coincidono. Esercizi 1. Espandi la funzione 2 in una serie di Fourier nell'intervallo (-i-, x) 2. Espandi la funzione in una serie di Fourier nell'intervallo (-tr, tr) 3. Espandi la funzione 4 in una serie di Fourier in l'intervallo (-tr, tr) nella serie di Fourier nella funzione intervallo (-jt, tr) 5. Espandi la funzione f(x) = x + x in una serie di Fourier nell'intervallo (-tr, tr). 6. Espandi la funzione n in una serie di Fourier nell'intervallo (-jt, tr) 7. Espandi la funzione /(x) = sin2 x in una serie di Fourier nell'intervallo (-tr, x). 8. Espandi la funzione f(x) = y in una serie di Fourier nell'intervallo (-tr, jt) 9. Espandi la funzione f(x) = | peccato x|. 10. Espandi la funzione f(x) = § in una serie di Fourier nell'intervallo (-π-, π). 11. Espandi la funzione f(x) = sin § in una serie di Fourier nell'intervallo (-tr, tr). 12. Espandi la funzione f(x) = n -2x, data nell'intervallo (0, x), in una serie di Fourier, estendendola nell'intervallo (-x, 0): a) in modo uniforme; b) in modo strano. 13. Espandi la funzione /(x) = x2, data nell'intervallo (0, x), in una serie di Fourier in seno. 14. Espandi la funzione /(x) = 3, data nell'intervallo (-2,2), in una serie di Fourier. 15. Espandi la funzione f(x) = |x|, data nell'intervallo (-1,1), in una serie di Fourier. 16. Espandi la funzione f(x) = 2x, specificata nell'intervallo (0,1), in una serie di Fourier in seno.

La serie di Fourier di una funzione periodica pari f(x) con periodo 2p contiene solo termini con coseni (cioè non contiene termini con seni) e può includere un termine costante. Quindi,

dove sono i coefficienti della serie di Fourier,

Espansione in serie di Fourier nei seni

La serie di Fourier di una funzione periodica dispari f (x) con periodo 2p contiene solo termini con seni (cioè non contiene termini con coseni).

Quindi,

dove sono i coefficienti della serie di Fourier,

Serie di Fourier a mezzo ciclo

Se una funzione è definita per un intervallo, ad esempio da 0 a p, e non solo da 0 a 2p, può essere espansa in una serie solo in seni o solo in coseni. La serie di Fourier risultante viene chiamata vicino Fourier SU mezzo ciclo

Se vuoi ottenere la scomposizione Fourier SU mezzo ciclo Di coseni funzioni f (x) nell'intervallo da 0 a p, allora è necessario costruire una funzione periodica pari. Nella fig. Di seguito è riportata la funzione f (x) = x, costruita sull'intervallo da x = 0 a x = p. Poiché la funzione pari è simmetrica rispetto all'asse f (x), tracciamo la linea AB, come mostrato in Fig. sotto. Se assumiamo che al di fuori dell'intervallo considerato la forma triangolare risultante sia periodica con periodo 2p, il grafico finale sarà simile a questo: nella fig. sotto. Poiché dobbiamo ottenere lo sviluppo di Fourier in coseni, come prima, calcoliamo i coefficienti di Fourier a o e a n

Se hai bisogno di ottenere decomposizione Fourier SU mezzo ciclo Di seni funzioni f (x) nell'intervallo da 0 a p, allora è necessario costruire una funzione periodica dispari. Nella fig. Di seguito è riportata la funzione f (x) =x, costruita sull'intervallo da x=0 a x=p. Poiché la funzione dispari è simmetrica rispetto all'origine, costruiamo la retta CD, come mostrato in Fig.

Se assumiamo che al di fuori dell'intervallo considerato il segnale a dente di sega risultante sia periodico con periodo 2p, allora il grafico finale avrà la forma mostrata in Fig. Poiché dobbiamo ottenere l'espansione di Fourier del semiciclo in termini di seno, come prima, calcoliamo il coefficiente di Fourier. B

Ministero dell'Istruzione Generale e Professionale

Università statale del turismo di Sochi

e attività di resort

Istituto Pedagogico

Facoltà di Matematica

Dipartimento di Matematica Generale

LAVORO DI LAUREA

Serie di Fourier e loro applicazioni

Nella fisica matematica.

Completato da: studente del 5° anno

firma dell’istruzione a tempo pieno

Specialità 010100

"Matematica"

Kasperova N.S.

ID studente n. 95471

Supervisore scientifico: professore associato, candidato.

firma tecnica scienze

Pozin P.A.

Soči, 2000

1. Introduzione.

2. Il concetto di serie di Fourier.

2.1. Determinazione dei coefficienti della serie di Fourier.

2.2. Integrali di funzioni periodiche.

3. Segni di convergenza delle serie di Fourier.

3.1. Esempi di sviluppo di funzioni in serie di Fourier.

4. Cenni sullo sviluppo in serie di Fourier di una funzione periodica

5. Serie di Fourier per funzioni pari e dispari.

6. Serie di Fourier per funzioni con periodo 2 l .

7. Sviluppo in serie di Fourier di una funzione non periodica.

Introduzione.

Jean Baptiste Joseph Fourier - matematico francese, membro dell'Accademia delle scienze di Parigi (1817).

I primi lavori di Fourier riguardavano l'algebra. Già nelle lezioni del 1796 presentò un teorema sul numero delle radici reali di un'equazione algebrica compresa tra confini dati (pubblicato nel 1820), a lui intitolato; una soluzione completa al numero di radici reali di un'equazione algebrica fu ottenuta nel 1829 da J.S.F. Per aggressione. Nel 1818 Fourier investigò la questione delle condizioni per l'applicabilità del metodo di soluzione numerica delle equazioni sviluppato da Newton, non conoscendo risultati simili ottenuti nel 1768 dal matematico francese J.R. Murailem. Il risultato del lavoro di Fourier sui metodi numerici per la risoluzione delle equazioni è "Analisi delle equazioni definite", pubblicato postumo nel 1831.

La principale area di studio di Fourier era la fisica matematica. Nel 1807 e nel 1811 presentò all'Accademia delle Scienze di Parigi le sue prime scoperte sulla teoria della propagazione del calore nei solidi e nel 1822 pubblicò la famosa opera "Teoria analitica del calore", che giocò un ruolo importante nella successiva storia dell'energia. matematica. Questa è la teoria matematica della conduttività termica. A causa della generalità del metodo, questo libro divenne la fonte di tutti i moderni metodi di fisica matematica. In questo lavoro Fourier derivò l'equazione differenziale della conducibilità termica e sviluppò le idee delineate in precedenza da D. Bernoulli; sviluppò un metodo per separare le variabili (metodo di Fourier) per risolvere l'equazione del calore in determinate condizioni al contorno, che applicò a un numero di casi particolari (cubo, cilindro, ecc.). Questo metodo si basa sulla rappresentazione delle funzioni mediante serie trigonometriche di Fourier.

Le serie di Fourier sono ora diventate uno strumento ben sviluppato nella teoria delle equazioni alle derivate parziali per risolvere problemi ai limiti.

1. Il concetto di serie di Fourier.(pag. 94, Uvarenkov)

Le serie di Fourier svolgono un ruolo importante nella fisica matematica, nella teoria dell'elasticità, nell'ingegneria elettrica e in particolare nel loro caso speciale: le serie trigonometriche di Fourier.

Una serie trigonometrica è una serie della forma

o, simbolicamente:

(1)

dove ω, a 0, a 1, …, a n, …, b 0, b 1, …, b n, … sono numeri costanti (ω>0).

Storicamente, alcuni problemi di fisica hanno portato allo studio di tali serie, ad esempio il problema delle vibrazioni delle corde (XVIII secolo), il problema delle regolarità nei fenomeni di conduzione del calore, ecc. Nelle applicazioni, considerazione delle serie trigonometriche , è principalmente associato al compito di rappresentare un dato movimento, descritto dall'equazione y = ƒ(χ), in

sotto forma di somma delle oscillazioni armoniche più semplici, spesso prese in numero infinitamente grande, cioè come somma di una serie della forma (1).

Si arriva quindi al seguente problema: scoprire se per una data funzione ƒ(x) su un dato intervallo esiste una serie (1) che convergerebbe su questo intervallo a questa funzione. Se ciò è possibile, allora dicono che su questo intervallo la funzione ƒ(x) si sviluppa in una serie trigonometrica.

La serie (1) converge in un punto x 0, a causa della periodicità delle funzioni

(n=1,2,..), risulterà convergente in tutti i punti della forma (m è un intero qualsiasi), e quindi la sua somma S(x) sarà (nella regione di convergenza della serie ) una funzione periodica: se S n ( x) è l'ennesima somma parziale di questa serie, allora abbiamo

e quindi

, cioè S(x 0 +T)=S(x 0). Pertanto, parlando dell'espansione di una funzione ƒ(x) in una serie della forma (1), assumeremo ƒ(x) come una funzione periodica.

2. Determinazione dei coefficienti di serie mediante formule di Fourier.

Sia una funzione periodica ƒ(x) con periodo 2π tale da essere rappresentata da una serie trigonometrica convergente a una data funzione nell'intervallo (-π, π), ovvero sia la somma di questa serie:

. (2)

Supponiamo che l'integrale della funzione a sinistra di questa uguaglianza sia uguale alla somma degli integrali dei termini di questa serie. Ciò sarà vero se assumiamo che la serie di numeri composta dai coefficienti di una data serie trigonometrica sia assolutamente convergente, cioè la serie di numeri positivi converge

(3)

La serie (1) è maggiorizzabile e può essere integrata termine per termine nell'intervallo (-π, π). Integriamo entrambi i lati dell'uguaglianza (2):

.

Valutiamo separatamente ciascun integrale che appare a destra:

, , .

Così,

, Dove . (4)

Stima dei coefficienti di Fourier.(Bugrov)

Teorema 1. Sia la funzione ƒ(x) del periodo 2π a derivata continua ƒ ( s) (x) ordine s, soddisfacendo la disuguaglianza sull'intero asse reale:

│ ƒ (s) (x)│≤ M s ; (5)

quindi i coefficienti di Fourier della funzione ƒ soddisfare la disuguaglianza

(6)

Prova. Integrando per parti e tenendo conto di ciò

ƒ(-π) = ƒ(π), abbiamo

Integrando sequenzialmente il membro destro della (7), tenendo conto che le derivate ƒ ΄, …, ƒ (s-1) sono continue e assumono gli stessi valori nei punti t = -π e t = π, come oltre alla stima (5), si ottiene la prima stima (6).

La seconda stima (6) si ottiene in modo simile.

Teorema 2. Per i coefficienti di Fourier ƒ(x) vale la seguente disuguaglianza:

(8)

Prova. Abbiamo

Serie di Fourier di funzioni periodiche con periodo 2π.

La serie di Fourier permette di studiare le funzioni periodiche scomponendole in componenti. Correnti e tensioni alternate, spostamenti, velocità e accelerazione dei manovellismi e onde acustiche sono tipici esempi pratici dell'uso delle funzioni periodiche nei calcoli ingegneristici.

Lo sviluppo in serie di Fourier si basa sul presupposto che tutte le funzioni di significato pratico nell'intervallo -π ≤x≤ π possano essere espresse sotto forma di serie trigonometriche convergenti (una serie è considerata convergente se la successione di somme parziali composta dai suoi termini converge):

Notazione standard (=ordinaria) attraverso la somma di sinx e cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

dove a o, a 1,a 2,...,b 1,b 2,.. sono costanti reali, cioè

Dove, per l'intervallo da -π a π, i coefficienti della serie di Fourier si calcolano utilizzando le formule:

Si chiamano i coefficienti a o , a n e b n Coefficienti di Fourier, e se possono essere trovati, allora viene chiamata la serie (1). accanto a Fourier, corrispondente alla funzione f(x). Per la serie (1), il termine (a 1 cosx+b 1 sinx) è detto primo o armonica fondamentale,

Un altro modo per scrivere una serie è usare la relazione acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Dove a o è una costante, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 sono le ampiezze delle varie componenti, ed è uguale a a n =arctg a n /b n.

Per la serie (1), il termine (a 1 cosx+b 1 sinx) oppure c 1 sin(x+α 1) è detto primo o armonica fondamentale,(a 2 cos2x+b 2 sin2x) oppure c 2 sin(2x+α 2) si chiama seconda armonica e così via.

Per rappresentare accuratamente un segnale complesso è necessario in genere un numero infinito di termini. Tuttavia, in molti problemi pratici è sufficiente considerare solo i primi termini.

Serie di Fourier di funzioni non periodiche con periodo 2π.

Espansione di funzioni non periodiche.

Se la funzione f(x) è non periodica, significa che non può essere sviluppata in una serie di Fourier per tutti i valori di x. Tuttavia, è possibile definire una serie di Fourier che rappresenta una funzione su qualsiasi intervallo di larghezza 2π.

Data una funzione non periodica, è possibile costruire una nuova funzione selezionando valori di f(x) entro un certo intervallo e ripetendoli al di fuori di tale intervallo a intervalli di 2π. Poiché la nuova funzione è periodica con periodo 2π, può essere espansa in una serie di Fourier per tutti i valori di x. Ad esempio, la funzione f(x)=x non è periodica. Tuttavia, se è necessario espanderlo in una serie di Fourier nell'intervallo da o a 2π, allora al di fuori di questo intervallo viene costruita una funzione periodica con un periodo di 2π (come mostrato nella figura seguente).

Per funzioni non periodiche come f(x)=x, la somma della serie di Fourier è uguale al valore di f(x) in tutti i punti in un dato intervallo, ma non è uguale a f(x) per i punti fuori portata. Per trovare la serie di Fourier di una funzione non periodica nell'intervallo 2π, viene utilizzata la stessa formula dei coefficienti di Fourier.

Funzioni pari e dispari.

Dicono che la funzione y=f(x) Anche, se f(-x)=f(x) per tutti i valori di x. I grafici delle funzioni pari sono sempre simmetrici rispetto all'asse y (cioè sono immagini speculari). Due esempi di funzioni pari: y=x2 e y=cosx.

Dicono che la funzione y=f(x) strano, se f(-x)=-f(x) per tutti i valori di x. I grafici delle funzioni dispari sono sempre simmetrici rispetto all'origine.

Molte funzioni non sono né pari né dispari.

Espansione in serie di Fourier in coseni.

La serie di Fourier di una funzione periodica pari f(x) con periodo 2π contiene solo termini coseno (cioè nessun termine seno) e può includere un termine costante. Quindi,

dove sono i coefficienti della serie di Fourier,

La serie di Fourier di una funzione periodica dispari f(x) con periodo 2π contiene solo termini con seni (cioè non contiene termini con coseni).

Quindi,

dove sono i coefficienti della serie di Fourier,

Serie di Fourier a mezzo ciclo.

Se una funzione è definita per un intervallo, ad esempio da 0 a π, e non solo da 0 a 2π, può essere espansa in una serie solo in seni o solo in coseni. La serie di Fourier risultante viene chiamata vicino a Fourier a metà ciclo.

Se vuoi ottenere la scomposizione Mezzo ciclo di Fourier per coseni funzioni f(x) nell'intervallo da 0 a π, allora è necessario costruire una funzione periodica pari. Nella fig. Di seguito è riportata la funzione f(x)=x, costruita sull'intervallo da x=0 a x=π. Poiché la funzione pari è simmetrica rispetto all'asse f(x), tracciamo la linea AB, come mostrato in Fig. sotto. Se assumiamo che al di fuori dell'intervallo considerato la forma triangolare risultante sia periodica con periodo 2π, il grafico finale sarà simile a questo: nella fig. sotto. Poiché dobbiamo ottenere lo sviluppo di Fourier in coseni, come prima, calcoliamo i coefficienti di Fourier a o e a n

Se hai bisogno di ottenere Espansione del seno a semiciclo di Fourier funzioni f(x) nell'intervallo da 0 a π, allora è necessario costruire una funzione periodica dispari. Nella fig. Di seguito è riportata la funzione f(x)=x, costruita sull'intervallo da x=0 a x=π. Poiché la funzione dispari è simmetrica rispetto all'origine, costruiamo la retta CD, come mostrato in Fig. Se assumiamo che al di fuori dell’intervallo considerato il segnale a dente di sega risultante sia periodico con periodo 2π, allora il grafico finale avrà la forma mostrata in Fig. Poiché dobbiamo ottenere l'espansione di Fourier del semiciclo in termini di seno, come prima, calcoliamo il coefficiente di Fourier. B

Serie di Fourier per un intervallo arbitrario.

Sviluppo di una funzione periodica con periodo L.

La funzione periodica f(x) si ripete quando x aumenta di L, cioè f(x+L)=f(x). Il passaggio dalle funzioni con periodo 2π precedentemente considerate alle funzioni con periodo L è abbastanza semplice, poiché può essere effettuato mediante un cambio di variabile.

Per trovare la serie di Fourier della funzione f(x) nell'intervallo -L/2≤x≤L/2, introduciamo una nuova variabile u in modo che la funzione f(x) abbia un periodo di 2π rispetto a u. Se u=2πx/L, allora x=-L/2 per u=-π e x=L/2 per u=π. Sia anche f(x)=f(Lu/2π)=F(u). La serie di Fourier F(u) ha la forma

(I limiti di integrazione possono essere sostituiti da qualsiasi intervallo di lunghezza L, ad esempio da 0 a L)

Serie di Fourier su semiciclo per funzioni specificate nell'intervallo L≠2π.

Per la sostituzione u=πх/L, l'intervallo da x=0 a x=L corrisponde all'intervallo da u=0 a u=π. Di conseguenza la funzione può essere sviluppata in una serie solo in coseni o solo in seni, cioè V Serie di Fourier a mezzo ciclo.

L'espansione del coseno nell'intervallo da 0 a L ha la forma